


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-9-2021
Date: 30-11-2021
Date: 11-10-2021
|
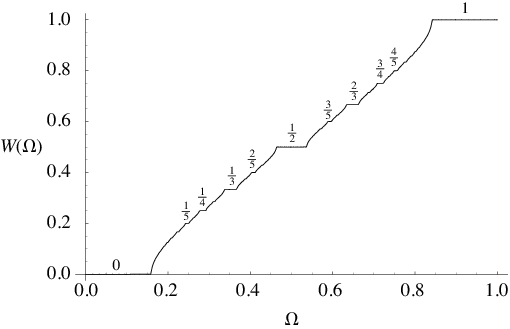
A plot of the map winding number 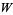 resulting from mode locking as a function of
resulting from mode locking as a function of 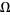 for the circle map
for the circle map
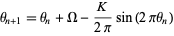 |
(1) |
with 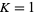 . (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument
. (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument 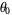 .) At each value of
.) At each value of 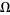 , the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval
, the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline6.gif) onto
onto ![[0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline7.gif) , but is constant almost everywhere (i.e., except on a Cantor set).
, but is constant almost everywhere (i.e., except on a Cantor set).
For 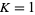 , the measure of quasiperiodic states (
, the measure of quasiperiodic states (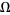 irrational) on the
irrational) on the 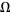 -axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase
-axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase 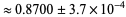 .
.
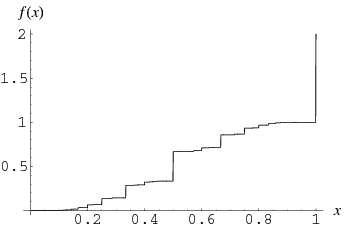
Another type of devil's staircase occurs for the sum
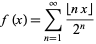 |
(2) |
for ![x in [0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline12.gif) , where
, where 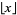 is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational
is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational  but discontinuous at every rational
but discontinuous at every rational  .
. 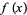 is irrational iff
is irrational iff  is, and if
is, and if  is irrational, then
is irrational, then 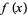 is transcendental. If
is transcendental. If 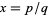 is rational, then
is rational, then
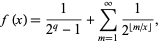 |
(3) |
while if  is irrational,
is irrational,
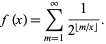 |
(4) |
Even more amazingly, for irrational  with simple continued fraction
with simple continued fraction ![[0,a_1,a_2,...]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline23.gif) and convergents
and convergents 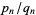 ,
,
![f(x)=[0,A_1,A_2,A_3,...],](https://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation5.gif) |
(5) |
where
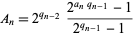 |
(6) |
(Bailey and Crandall 2001). This gives the beautiful relation to the Rabbit constant
![f(phi^(-1))=[0,2^(F_0),2^(F_1),2^(F_2),...],](https://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation7.gif) |
(7) |
where 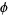 is the golden ratio and
is the golden ratio and 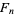 is a Fibonacci number.
is a Fibonacci number.
REFERENCES:
Adams, W. W. "A Remarkable Class of Continued Fractions." Proc. Amer. Math. Soc. 65, 194-198, 1977.
Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Böhmer, P. E. "Über die Transcendenz gewisser dyadischer Brüche." Math. Ann. 96, 367-377, 1926a.
Böhmer, P. E. Erratum to "Über die Transcendenz gewisser dyadischer Brüche." Math. Ann. 96, 735, 1926b.
Borwein, J. and Borwein, P. "On the Generating Function of the Integer Part of 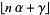 ." J. Number Th. 43, 293-318, 1993.
." J. Number Th. 43, 293-318, 1993.
Bowman, D. "A New Generalization of Davison's Theorem." Fib. Quart. 26, 40-45, 1988.
Bowman, D. "Approximation of 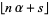 and the Zero of
and the Zero of 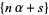 ." J. Number Th. 50, 128-144, 1995.
." J. Number Th. 50, 128-144, 1995.
Danilov, L. V. "Some Classes of Transcendental Numbers." Math. Notes Acad. Sci. USSR 12, 524-527, 1974.
Davison, J. L. "A Series and Its Associated Continued Fraction." Proc. Amer. Math. Soc. 63, 29-32, 1977.
Devaney, R. L. An Introduction to Chaotic Dynamical Systems. Redwood City, CA: Addison-Wesley, pp. 109-110, 1987.
Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 82-83 and 286-287, 1983.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, 1993.
Rasband, S. N. "The Circle Map and the Devil's Staircase." §6.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 128-132, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|