


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-10-2021
Date: 19-12-2021
Date: 7-10-2021
|
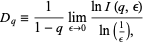 |
(1) |
where
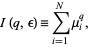 |
(2) |
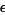 is the box size, and
is the box size, and 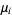 is the natural measure.
is the natural measure.
The capacity dimension (a.k.a. box-counting dimension) is given by 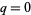 ,
,
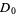 |
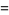 |
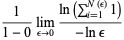 |
(3) |
 |
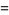 |
![-lim_(epsilon->0)(ln[N(epsilon)])/(lnepsilon).](https://mathworld.wolfram.com/images/equations/q-Dimension/Inline9.gif) |
(4) |
If all 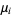 s are equal, then the capacity dimension is obtained for any
s are equal, then the capacity dimension is obtained for any 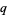 .
.
The information dimension corresponds to 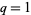 and is given by
and is given by
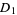 |
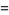 |
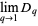 |
(5) |
 |
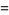 |
![lim_(q->1)(lim_(epsilon->0)(ln[sum_(i=1)^(N(epsilon))mu_i^q])/(-lnepsilon))/(1-q)](https://mathworld.wolfram.com/images/equations/q-Dimension/Inline18.gif) |
(6) |
 |
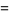 |
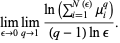 |
(7) |
But for the numerator,
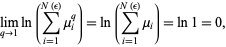 |
(8) |
and for the denominator, 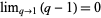 , so use l'Hospital's rule to obtain
, so use l'Hospital's rule to obtain
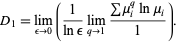 |
(9) |
Therefore,
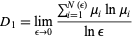 |
(10) |
(Ott 1993, p. 79).
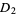 is called the correlation dimension.
is called the correlation dimension.
If 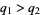 , then
, then
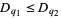 |
(11) |
(Ott 1993, p. 79).
REFERENCES:
Grassberger, P. "Generalized Dimensions of Strange Attractors." Phys. Lett. A 97, 227, 1983.
Hentschel, H. G. E. and Procaccia, I. "The Infinite Number of Generalized Dimensions of Fractals and Strange Attractors." Physica D 8, 435, 1983.
Ott, E. "Measure and the Spectrum of  Dimensions." §3.3 in Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 78-81, 1993.
Dimensions." §3.3 in Chaos in Dynamical Systems. New York: Cambridge University Press, pp. 78-81, 1993.
Rényi, A. Probability Theory. Amsterdam, Netherlands: North-Holland, 1970.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|