
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-7-2021
Date: 11-8-2021
Date: 20-5-2021
|
For 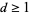 ,
, 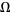 an open subset of
an open subset of 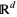 ,
, ![p in [1;+infty]](https://mathworld.wolfram.com/images/equations/SobolevSpace/Inline4.gif) and
and 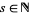 , the Sobolev space
, the Sobolev space 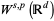 is defined by
is defined by
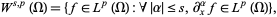 |
(1) |
where 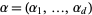 ,
, 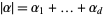 , and the derivatives
, and the derivatives 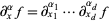 are taken in a weak sense.
are taken in a weak sense.
When endowed with the norm
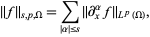 |
(2) |
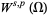 is a Banach space.
is a Banach space.
In the special case 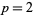 ,
, 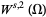 is denoted by
is denoted by 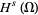 . This space is a Hilbert space for the inner product
. This space is a Hilbert space for the inner product
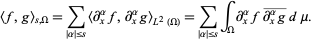 |
(3) |
Sobolev spaces play an important role in the theory of partial differential equations.
REFERENCES:
Mazja, V. Sobolev Spaces. New York: Springer-Verlag, 1985.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|