
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-7-2021
Date: 31-5-2021
Date: 8-5-2021
|
For any Abelian group 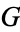 and any natural number
and any natural number 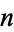 , there is a unique space (up to homotopy type) such that all homotopy groups except for the
, there is a unique space (up to homotopy type) such that all homotopy groups except for the 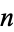 th are trivial (including the 0th homotopy groups, meaning the space is pathwise-connected), and the
th are trivial (including the 0th homotopy groups, meaning the space is pathwise-connected), and the 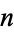 th homotopy group is isomorphic to the group
th homotopy group is isomorphic to the group 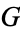 . In the case where
. In the case where 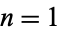 , the group
, the group  can be non-Abelian as well.
can be non-Abelian as well.
Eilenberg-Mac Lane spaces have many important applications. One of them is that every topological space has the homotopy type of an iterated fibration of Eilenberg-Mac Lane spaces (called a Postnikov system). In addition, there is a spectral sequence relating the cohomology of Eilenberg-Mac Lane spaces to the homotopy groups of spheres.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|