
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2021
Date: 6-5-2021
Date: 17-6-2021
|
The convexity coefficient 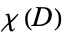 of a region
of a region 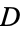 is the probability that the line segment connecting two random points in
is the probability that the line segment connecting two random points in 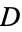 is contained entirely within
is contained entirely within 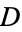 . For a convex region,
. For a convex region, 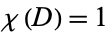 .
.
For 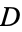 a subset of
a subset of 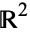 , let the area of the visible region of a point
, let the area of the visible region of a point 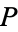 be denoted
be denoted 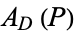 , and let the area of
, and let the area of 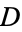 be denoted
be denoted 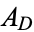 . Then
. Then
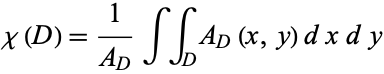 |
(Hodge et al. 2010).
The convexity coefficient is in general hard to compute exactly for concave regions even of simple shape. One closed form is that of an annulus with inner radius 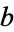 and outer radius
and outer radius 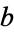 , which has
, which has
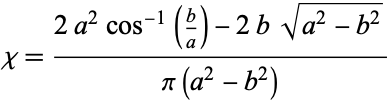 |
(Hodge et al. 2010).
REFERENCES:
Hodge, J.; Marshall, E.; and Patterson, G. "Gerrymandering and Convexity." Coll. Math. J. 41, 312-324, 2010.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تناقش تحديد الرؤية البصرية الخاصة بحفل تخرج طلبة الجامعات العراقية
|
|
|