


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-6-2021
Date: 6-6-2021
Date: 14-7-2021
|
For 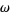 a differential (k-1)-form with compact support on an oriented
a differential (k-1)-form with compact support on an oriented 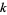 -dimensional manifold with boundary
-dimensional manifold with boundary 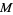 ,
,
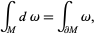 |
(1) |
where 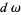 is the exterior derivative of the differential form
is the exterior derivative of the differential form 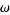 . When
. When 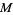 is a compact manifold without boundary, then the formula holds with the right hand side zero.
is a compact manifold without boundary, then the formula holds with the right hand side zero.
Stokes' theorem connects to the "standard" gradient, curl, and divergence theorems by the following relations. If 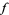 is a function on
is a function on 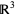 ,
,
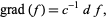 |
(2) |
where 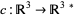 (the dual space) is the duality isomorphism between a vector space and its dual, given by the Euclidean inner product on
(the dual space) is the duality isomorphism between a vector space and its dual, given by the Euclidean inner product on 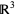 . If
. If 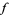 is a vector field on a
is a vector field on a 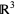 ,
,
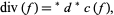 |
(3) |
where 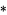 is the Hodge star operator. If
is the Hodge star operator. If 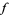 is a vector field on
is a vector field on 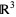 ,
,
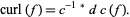 |
(4) |
With these three identities in mind, the above Stokes' theorem in the three instances is transformed into the gradient, curl, and divergence theorems respectively as follows. If 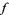 is a function on
is a function on 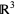 and
and 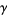 is a curve in
is a curve in 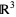 , then
, then
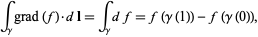 |
(5) |
which is the gradient theorem. If 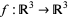 is a vector field and
is a vector field and 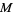 an embedded compact 3-manifold with boundary in
an embedded compact 3-manifold with boundary in 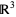 , then
, then
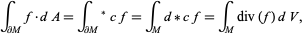 |
(6) |
which is the divergence theorem. If 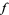 is a vector field and
is a vector field and 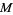 is an oriented, embedded, compact 2-manifold with boundary in
is an oriented, embedded, compact 2-manifold with boundary in 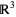 , then
, then
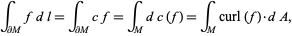 |
(7) |
which is the curl theorem.
de Rham cohomology is defined using differential k-forms. When 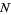 is a submanifold (without boundary), it represents a homology class. Two closed forms represent the same cohomology class if they differ by an exact form,
is a submanifold (without boundary), it represents a homology class. Two closed forms represent the same cohomology class if they differ by an exact form, 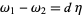 . Hence,
. Hence,
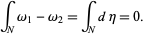 |
(8) |
Therefore, the evaluation of a cohomology class on a homology class is well-defined.
Physicists generally refer to the curl theorem
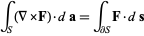 |
(9) |
as Stokes' theorem.
REFERENCES:
Morse, P. M. and Feshbach, H. "Stokes' Theorem." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 43, 1953.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|