


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-7-2021
Date: 5-6-2021
Date: 13-7-2021
|
The smallest number of times 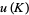 a knot
a knot 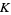 must be passed through itself to untie it. Lower bounds can be computed using relatively straightforward techniques, but it is in general difficult to determine exact values. Many unknotting numbers can be determined from a knot's knot signature. A knot with unknotting number 1 is a prime knot (Scharlemann 1985). It is not always true that the unknotting number is achieved in a projection with the minimal number of crossings.
must be passed through itself to untie it. Lower bounds can be computed using relatively straightforward techniques, but it is in general difficult to determine exact values. Many unknotting numbers can be determined from a knot's knot signature. A knot with unknotting number 1 is a prime knot (Scharlemann 1985). It is not always true that the unknotting number is achieved in a projection with the minimal number of crossings.
The following table is from Kirby (1997, pp. 88-89), with the values for 10-139 and 10-152 taken from Kawamura (1998). In the following table, Kirby's (1997, p. 88) value 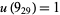 has been corrected to reflect the fact that
has been corrected to reflect the fact that 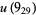 is only currently known to be 1 or 2 (Kawauchi 1996, p. 271). The value
is only currently known to be 1 or 2 (Kawauchi 1996, p. 271). The value 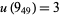 has been computed by Stoimenow (2002). The unknotting numbers for 10-154 and 10-161 can be found using the slice-Bennequin inequality (Stoimenow 1998).
has been computed by Stoimenow (2002). The unknotting numbers for 10-154 and 10-161 can be found using the slice-Bennequin inequality (Stoimenow 1998).
Knots for which the unknotting number is not known are 10-11, 10-47, 10-51, 10-54, 10-61, 10-76, 10-77, 10-79, 10-100 (Cha and Livingston 2008).
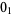 |
0 | 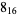 |
2 | 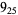 |
2 | 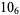 |
3 | 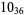 |
2 | 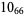 |
3 | 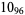 |
2 | 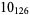 |
2 | 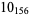 |
1 |
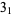 |
1 | 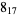 |
1 | 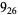 |
1 | 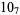 |
1 | 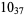 |
2 | 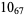 |
2 | 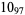 |
2 | 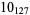 |
2 | 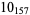 |
2 |
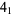 |
1 | 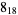 |
2 | 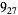 |
1 | 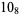 |
2 | 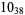 |
2 | 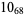 |
2 | 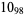 |
2 | 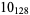 |
3 | 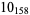 |
2 |
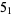 |
2 | 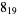 |
3 | 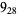 |
1 | 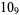 |
1 | 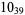 |
2 | 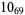 |
2 | 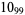 |
2 | 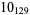 |
1 | 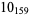 |
1 |
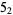 |
1 | 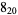 |
1 | 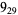 |
2 | 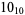 |
1 | 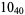 |
2 | 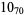 |
2 | 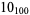 |
? | 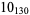 |
2 | 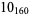 |
2 |
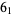 |
1 | 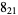 |
1 | 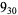 |
1 | 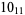 |
? | 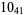 |
2 | 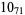 |
1 | 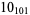 |
3 | 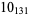 |
1 | 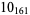 |
3 |
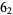 |
1 | 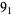 |
4 | 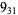 |
2 | 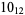 |
2 | 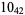 |
1 | 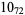 |
2 | 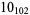 |
1 | 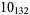 |
1 | 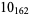 |
2 |
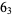 |
1 | 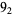 |
1 | 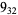 |
2 | 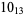 |
2 | 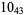 |
2 | 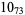 |
1 | 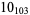 |
3 | 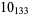 |
1 | 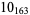 |
2 |
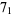 |
3 | 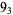 |
3 | 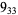 |
1 | 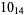 |
2 | 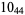 |
1 | 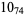 |
2 | 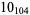 |
1 | 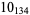 |
3 | 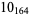 |
1 |
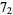 |
1 | 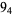 |
2 | 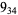 |
1 | 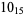 |
2 | 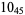 |
2 | 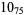 |
2 | 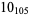 |
2 | 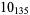 |
2 | 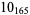 |
2 |
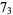 |
2 | 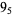 |
2 | 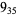 |
3 | 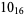 |
2 | 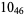 |
3 | 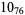 |
? | 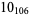 |
2 | 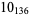 |
1 | ||
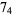 |
2 | 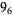 |
3 | 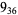 |
2 | 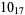 |
1 | 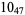 |
? | 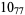 |
? | 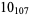 |
1 | 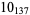 |
1 | ||
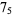 |
2 | 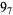 |
2 | 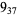 |
2 | 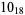 |
1 | 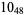 |
2 | 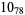 |
2 | 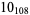 |
2 | 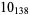 |
2 | ||
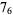 |
1 | 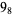 |
2 | 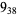 |
3 | 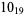 |
2 | 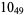 |
3 | 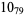 |
? | 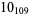 |
2 | 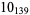 |
4 | ||
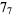 |
1 | 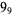 |
3 | 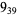 |
1 | 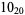 |
2 | 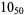 |
2 | 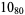 |
3 | 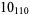 |
2 | 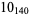 |
2 | ||
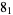 |
1 | 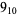 |
3 | 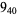 |
2 | 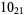 |
2 | 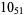 |
? | 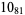 |
2 | 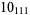 |
2 | 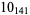 |
1 | ||
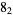 |
2 | 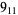 |
2 | 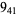 |
2 | 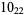 |
2 | 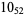 |
2 | 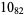 |
1 | 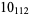 |
2 | 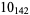 |
3 | ||
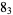 |
2 | 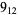 |
1 | 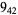 |
1 | 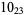 |
1 | 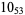 |
3 | 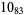 |
2 | 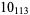 |
1 | 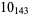 |
1 | ||
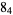 |
2 | 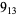 |
3 | 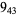 |
2 | 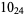 |
2 | 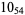 |
? | 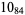 |
1 | 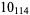 |
1 | 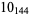 |
2 | ||
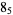 |
2 | 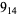 |
1 | 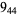 |
1 | 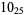 |
2 | 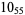 |
2 | 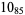 |
2 | 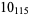 |
2 | 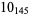 |
2 | ||
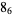 |
2 | 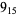 |
2 | 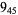 |
1 | 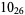 |
1 | 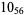 |
2 | 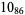 |
2 | 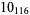 |
2 | 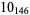 |
1 | ||
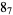 |
1 | 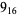 |
3 | 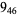 |
2 | 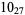 |
1 | 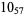 |
2 | 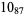 |
2 | 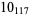 |
2 | 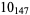 |
1 | ||
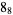 |
2 | 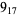 |
2 | 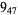 |
2 | 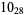 |
2 | 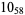 |
2 | 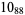 |
1 | 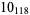 |
1 | 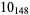 |
2 | ||
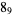 |
1 | 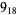 |
2 | 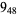 |
2 | 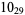 |
2 | 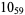 |
1 | 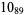 |
2 | 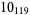 |
1 | 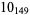 |
2 | ||
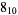 |
2 | 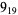 |
1 | 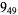 |
3 | 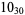 |
1 | 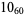 |
1 | 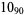 |
2 | 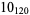 |
3 | 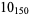 |
2 | ||
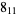 |
1 | 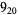 |
2 | 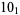 |
1 | 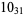 |
1 | 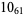 |
? | 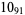 |
1 | 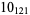 |
2 | 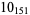 |
2 | ||
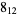 |
2 | 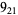 |
1 | 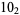 |
3 | 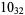 |
1 | 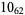 |
2 | 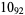 |
2 | 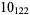 |
2 | 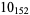 |
4 | ||
 |
1 | 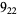 |
1 | 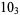 |
2 | 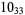 |
1 | 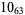 |
2 | 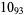 |
2 | 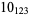 |
2 | 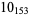 |
2 | ||
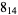 |
1 | 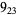 |
2 | 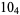 |
2 | 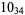 |
2 | 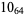 |
2 | 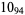 |
2 | 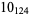 |
4 | 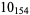 |
3 | ||
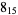 |
2 | 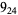 |
1 | 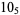 |
2 | 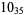 |
2 | 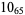 |
2 | 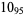 |
1 | 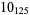 |
2 | 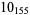 |
2 |
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 57-64, 1994.
Cha, J. C. and Livingston, C. "Unknown Values in the Table of Knots." 2008 May 16. https://arxiv.org/abs/math.GT/0503125.
Cipra, B. "From Knot to Unknot." What's Happening in the Mathematical Sciences, Vol. 2. Providence, RI: Amer. Math. Soc., pp. 8-13, 1994.
Kawamura, T. "The Unknotting Numbers of 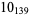 and
and 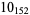 Are 4." Osaka J. Math. 35, 539-546, 1998.
Are 4." Osaka J. Math. 35, 539-546, 1998.
Kawauchi, A. "Knot Invariants." Appendix F.3 in A Survey of Knot Theory. Boston: Birkhäuser, 1996.
Kirby, R. (Ed.). "Problems in Low-Dimensional Topology." AMS/IP Stud. Adv. Math., 2.2, Geometric Topology (Athens, GA, 1993). Providence, RI: Amer. Math. Soc., pp. 35-473, 1997.
Scharlemann, M. "Unknotting Number One Knots Are Prime." Invent. Math. 82, 37-55, 1985.
Stoimenow, A. "Polynomial Values, the Linking Form, and Unknotting Numbers." https://www.math.toronto.edu/stoimeno/goer.ps.gz. Feb. 10, 2002.
Stoimenow, A. "Positive Knots, Closed Braids and the Jones Polynomial." https://www.math.toronto.edu/stoimeno/pos.ps.gz. Mar. 2, 2002.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|