Twist

The twist of a ribbon measures how much it twists around its axis and is defined as the integral of the incremental twist around the ribbon. A formula for the twist is given by

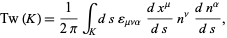(1)

where 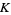 is parameterized by  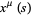for 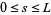 along the length of the knot by parameter 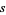, and the frame  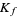associated with  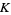is

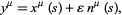(2)

where 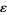 is a small parameter and  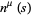is a unit vector field normal to the curve at  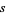(Kaul 1999).

Letting Lk be the linking number of the two components of a ribbon, Tw be the twist, and Wr be the writhe, then the calugareanu theorem states that

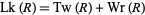(3)

(Adams 1994, p. 187).

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, 1994.

Kaul, R. K. "Topological Quantum Field Theories--A Meeting Ground for Physicists and Mathematicians." 15 Jul 1999. https://arxiv.org/abs/hep-th/9907119.