Taniyama-Shimura Conjecture

The Taniyama-Shimura conjecture, since its proof now sometimes known as the modularity theorem, is very general and important conjecture (and now theorem) connecting topology and number theory which arose from several problems proposed by Taniyama in a 1955 international mathematics symposium.

Let  be an elliptic curve whose equation has integer coefficients, let  be the so-called j-conductor of  and, for each , let  be the number appearing in the -function of . Then, in technical terms, the Taniyama-Shimura conjecture states that there exists a modular form of weight two and level  which is an eigenform under the Hecke operators and has a Fourier series .

In effect, the conjecture says that every rational elliptic curve is a modular form in disguise. Or, more formally, the conjecture suggests that, for every elliptic curve  over the rationals, there exist nonconstant modular functions  and  of the same level  such that

Equivalently, for every elliptic curve, there is a modular form with the same Dirichlet L-series.

In 1985, starting with a fictitious solution to Fermat's last theorem (the Frey curve), G. Frey showed that he could create an unusual elliptic curve which appeared not to be modular. If the curve were not modular, then this would show that if Fermat's last theorem were false, then the Taniyama-Shimura conjecture would also be false. Furthermore, if the Taniyama-Shimura conjecture is true, then so is Fermat's last theorem.

However, Frey did not actually prove that his curve was not modular. The conjecture that Frey's curve was not modular came to be called the "epsilon conjecture," and was quickly proved by Ribet (Ribet's theorem) in 1986, establishing a very close link between two mathematical structures (the Taniyama-Shimura conjecture and Fermat's last theorem) which appeared previously to be completely unrelated.

As of the early 1990s, most mathematicians believed that the Taniyama-Shimura conjecture was not accessible to proof. However, A. Wiles was not one of these. He attempted to establish the correspondence between the set of elliptic curves and the set of modular elliptic curves by showing that the number of each was the same. Wiles accomplished this by "counting" Galois representations and comparing them with the number of modular forms. In 1993, after a monumental seven-year effort, Wiles (almost) proved the Taniyama-Shimura conjecture for special classes of curves called semistable elliptic curves (which correspond to elliptic curves with squarefree conductors; Knapp 1999).

Wiles had tried to use horizontal Iwasawa theory to create a so-called class number formula, but was initially unsuccessful and therefore used instead an extension of a result of Flach based on ideas from Kolyvagin. However, there was a problem with this extension which was discovered during review of Wiles' manuscript in September 1993. Former student Richard Taylor came to Princeton in early 1994 to help Wiles patch up this error. After additional effort, Wiles discovered the reason that the Flach/Kolyvagin approach was failing, and also discovered that it was precisely what had prevented Iwasawa theory from working.

With this additional insight, Wiles was able to successfully complete the erroneous portion of the proof using Iwasawa theory, proving the semistable case of the Taniyama-Shimura conjecture (Taylor and Wiles 1995, Wiles 1995) and, at the same time, establishing Fermat's last theorem as a true theorem.

The existence of a proof of the full Taniyama-Shimura conjecture was announced at a conference by Kenneth Ribet on June, 21 1999 (Knapp 1999), and reported on National Public Radio's Weekend Edition on July 31, 1999. The proof was completed by Breuil et al. (2001) building on the earlier work of Wiles and Taylor (Mackenzie 1999, Morgan 1999). The best previous published result held for all conductors except those divisible by 27 (Conrad et al. 1999; Knapp 1999). The general Breuil et al. proof for all elliptic curves removed this restriction, in the process relying on Wiles' proof for rational elliptic curves.

REFERENCES:

American Mathematical Society. https://www.ams.org/new-in-math/10-1999-media.html#fermat.

Breuil, C.; Conrad, B.; Diamond, F.; and Taylor, R. "On the Modularity of Elliptic Curves Over 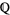: Wild 3-Adic Exercises." J. Amer. Math. Soc. 14, 843-939, 2001.

Conrad, B.; Diamond, F.; and Taylor, R. "Modularity of Certain Potentially Barsotti-Tate Galois Representations." J. Amer. Math. Soc. 12, 521-567, 1999.

Darmon, H. "A Proof of the Full Shimura-Taniyama-Weil Conjecture is Announced." Not. Amer. Math. Soc. 46, 1397-1406, 1999.

Ekeland, I. "Curves and Numbers." Nature 405, 748-749, 2000.

Knapp, A. W. "Proof Announced of Taniyama-Shimura-Weil Conjecture." Not. Amer. Math. Soc. 46, 863, 1999.

Lang, S. "Some History of the Shimura-Taniyama Conjecture." Not. Amer. Math. Soc. 42, 1301-1307, 1995.

Mackenzie, D. "Fermat's Last Theorem Extended." Science 285, 178, 1999.

Morgan, F. "Frank Morgan's Math Chat." https://www.maa.org/features/mathchat/mathchat_7_1_99.html. July 1, 1999.

Peterson, I. "Curving Beyond Fermat's Last Theorem." Sci. News 156, 221, Oct. 2, 1999.

Ribet, K. A. "From the Taniyama-Shimura Conjecture to Fermat's Last Theorem." Ann. Fac. Sci. Toulouse Math. 11, 116-139, 1990.

--. Science 285, 178, 1999.

Shimura, G. and Taniyama, Y. Complex Multiplication of Abelian Varieties and Its Applications to Number Theory. Tokyo: Mathematical Society of Japan, 1961.

Taylor, R. and Wiles, A. "Ring-Theoretic Properties of Certain Hecke Algebras." Ann. Math. 141, 553-572, 1995.

Wiles, A. "Modular Elliptic-Curves and Fermat's Last Theorem." Ann. Math. 141, 443-551, 1995.