المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Simplicial Homomorphism |
 1278
 07:01 مساءً
date: 17-5-2021 |
Author : Hatcher, A 
Book or Source : Algebraic Topology. Cambridge, England: Cambridge University Press, 2002. 
Page and Part : ...|
Read More
Date: 26-5-2021
1519
Date: 20-6-2021
1556
Date: 27-6-2021
1783
|
Let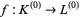 
be a bijective correspondence such that the vertices 
, ..., 
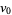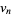of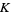 
span a simplex of 
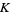iff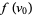 
, ..., 
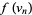span a simplex of 
. Then the induced simplicial map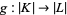 
is a homeomorphism, and the map 
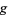is called a simplicial homeomorphism (Munkres 1993, p. 13).
REFERENCES:
Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2002.
Munkres, J. R. Elements of Algebraic Topology. New York: Perseus Books Pub., 1993.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
