


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-4-2021
Date: 17-4-2021
Date: 28-3-2021
|
A sequence of uncorrelated numbers 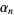 developed by Wiener (1926-1927). The numbers are constructed by beginning with
developed by Wiener (1926-1927). The numbers are constructed by beginning with
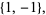 |
(1) |
then forming the outer product with 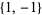 to obtain
to obtain
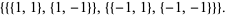 |
(2) |
This row is repeated twice, and its outer product is then taken to give
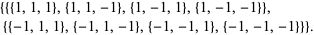 |
(3) |
This is then repeated four times. The procedure is repeated, and the result repeated eight times, and so on. The sequences from each stage are then concatenated to form the sequence 1, 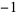 , 1, 1, 1,
, 1, 1, 1, 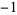 ,
, 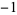 , 1,
, 1, 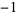 ,
, 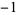 , 1, 1, 1,
, 1, 1, 1, 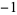 ,
, 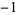 , 1,
, 1, 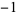 ,
, 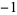 , ....
, ....
REFERENCES:
Papoulis, A. "The Wiener Numbers." The Fourier Integral and Its Applications. New York: McGraw-Hill, pp. 258-259, 1962.
Wiener, N. "The Spectrum of an Array and Its Applications to the Study of the Translation Properties of a Simple Class of Arithmetical Functions." J. Math. Phys. 6, 1926-1927.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|