


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-5-2021
Date: 24-2-2021
Date: 11-2-2021
|

In practice, the vertical offsets from a line (polynomial, surface, hyperplane, etc.) are almost always minimized instead of the perpendicular offsets. This provides a fitting function for the independent variable 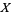 that estimates
that estimates 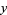 for a given
for a given  (most often what an experimenter wants), allows uncertainties of the data points along the
(most often what an experimenter wants), allows uncertainties of the data points along the  - and
- and 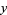 -axes to be incorporated simply, and also provides a much simpler analytic form for the fitting parameters than would be obtained using a fit based on perpendicular offsets.
-axes to be incorporated simply, and also provides a much simpler analytic form for the fitting parameters than would be obtained using a fit based on perpendicular offsets.
The residuals of the best-fit line for a set of 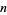 points using unsquared perpendicular distances
points using unsquared perpendicular distances 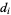 of points
of points 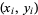 are given by
are given by
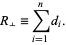 |
(1) |
Since the perpendicular distance from a line 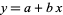 to point
to point 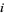 is given by
is given by
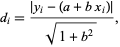 |
(2) |
the function to be minimized is
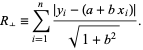 |
(3) |
Unfortunately, because the absolute value function does not have continuous derivatives, minimizing 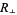 is not amenable to analytic solution. However, if the square of the perpendicular distances
is not amenable to analytic solution. However, if the square of the perpendicular distances
![R__|_^2=sum_(i=1)^n([y_i-(a+bx_i)]^2)/(1+b^2)](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/NumberedEquation4.gif) |
(4) |
is minimized instead, the problem can be solved in closed form. 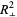 is a minimum when
is a minimum when
=0](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/NumberedEquation5.gif) |
(5) |
and
+sum_(i=1)^n([y_i-(a+bx_i)]^2(-1)(2b))/((1+b^2)^2)=0.](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/NumberedEquation6.gif) |
(6) |
The former gives
 |
 |
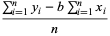 |
(7) |
 |
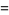 |
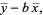 |
(8) |
and the latter
![(1+b^2)sum_(i=1)^n[y_i-(a+bx_i)]x_i+bsum_(i=1)^n[y_i-(a+bx_i)]^2=0.](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/NumberedEquation7.gif) |
(9) |
But
![[y-(a+bx)]^2](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/Inline19.gif) |
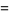 |
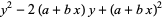 |
(10) |
 |
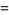 |
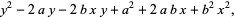 |
(11) |
so (10) becomes
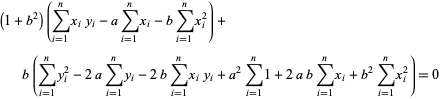 |
(12) |
![[(1+b^2)(-b)+b(b^2)]sum_(i=1)^(n)x_i^2+[(1+b^2)-2b^2]sum_(i=1)^(n)x_iy_i+bsum_(i=1)^(n)y_i^2+[-a(1+b^2)+2ab^2]sum_(i=1)^(n)x_i-2absum_(i=1)^(n)y_i+ba^2sum_(i=1)^(n)1=0](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/Inline26.gif) |
(13) |
 |
(14) |
Plugging (◇) into (14) then gives
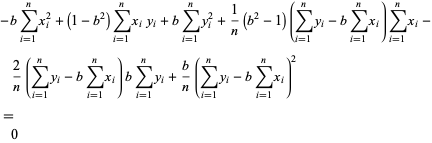 |
(15) |
After a fair bit of algebra, the result is
![b^2+(sum_(i=1)^(n)y_i^2-sum_(i=1)^(n)x_i^2+1/n[(sum_(i=1)^(n)x_i)^2-(sum_(i=1)^(n)y_i)^2])/(1/nsum_(i=1)^(n)x_isum_(i=1)^(n)y_i-sum_(i=1)^(n)x_iy_i)b-1=0.](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/NumberedEquation9.gif) |
(16) |
So define
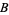 |
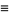 |
![1/2([sum_(i=1)^ny_i^2-1/n(sum_(i=1)^ny_i)^2]-[sum_(i=1)^nx_i^2-1/n(sum_(i=1)^nx_i)^2])/(1/nsum_(i=1)^nx_isum_(i=1)^ny_i-sum_(i=1)^nx_iy_i)](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPerpendicularOffsets/Inline30.gif) |
(17) |
 |
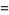 |
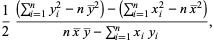 |
(18) |
and the quadratic formula gives
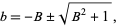 |
(19) |
with 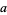 found using (◇). Note the rather unwieldy form of the best-fit parameters in the formulation. In addition, minimizing
found using (◇). Note the rather unwieldy form of the best-fit parameters in the formulation. In addition, minimizing 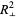 for a second- or higher-order polynomial leads to polynomial equations having higher order, so this formulation cannot be extended.
for a second- or higher-order polynomial leads to polynomial equations having higher order, so this formulation cannot be extended.
REFERENCES:
Sardelis, D. and Valahas, T. "Least Squares Fitting-Perpendicular Offsets." https://library.wolfram.com/infocenter/MathSource/5292/.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مجلةٌ عالميةٌ تنشر تفاصيل مشروع ملف تفويض المؤلِّفين العراقيين لحفظ التراث الفكري
|
|
|