


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-4-2021
Date: 25-4-2021
Date: 9-3-2021
|
A marked point process with mark space 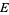 is a double sequence
is a double sequence
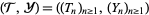 |
of 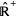 -valued random variables and
-valued random variables and 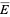 -valued random variables
-valued random variables 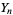 defined on a probability space
defined on a probability space 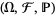 such that
such that 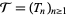 is a simple point process (SPP) and:
is a simple point process (SPP) and:
1. 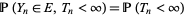 for
for 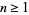 ;
;
2. 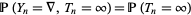 for
for 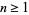 .
.
Here, 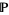 denotes probability,
denotes probability, 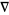 denotes the so-called irrelevant mark which is used to describe the mark of an event that never occurs, and
denotes the so-called irrelevant mark which is used to describe the mark of an event that never occurs, and 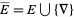 .
.
This definition is similar to the definition of an SPP in that it describes a sequence of time points marking the occurrence of events. The difference is that these events may be of different types where the type (i.e., the mark) of the 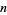 th event is denoted by
th event is denoted by 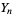 . Note that, because of the inclusion of the irrelevant mark
. Note that, because of the inclusion of the irrelevant mark 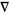 , marking will assign values
, marking will assign values 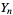 for all
for all 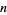 --even when
--even when 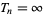 , i.e., when the
, i.e., when the 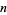 th event never occurs (Jacobsen 2006).
th event never occurs (Jacobsen 2006).
REFERENCES:
Jacobsen, M. Point Process Theory and Applications: Marked Point and Piecewise Deterministic Process. Boston: Birkhäuser, 2006.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|