


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-3-2021
Date: 9-3-2021
Date: 11-2-2021
|
Let 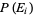 be the probability that
be the probability that 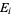 is true, and
is true, and 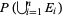 be the probability that at least one of
be the probability that at least one of 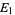 ,
, 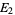 , ...,
, ..., 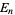 is true. Then "the" Bonferroni inequality, also known as Boole's inequality, states that
is true. Then "the" Bonferroni inequality, also known as Boole's inequality, states that
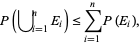 |
where 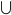 denotes the union. If
denotes the union. If 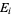 and
and 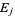 are disjoint sets for all
are disjoint sets for all 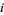 and
and 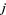 , then the inequality becomes an equality. A beautiful theorem that expresses the exact relationship between the probability of unions and probabilities of individual events is known as the inclusion-exclusion principle.
, then the inequality becomes an equality. A beautiful theorem that expresses the exact relationship between the probability of unions and probabilities of individual events is known as the inclusion-exclusion principle.
A slightly wider class of inequalities are also known as "Bonferroni inequalities."
REFERENCES:
Comtet, L. "Bonferroni Inequalities." §4.7 in Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 193-194, 1974.
Dohmen, K. Improved Bonferroni Inequalities with Applications: Inequalities and Identities of Inclusion-Exclusion Type. Berlin: Springer-Verlag, 2003.
Galambos, J. and Simonelli, I. Bonferroni-Type Inequalities with Applications. New York: Springer-Verlag, 1996.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|