


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2021
Date: 8-3-2021
Date: 25-4-2021
|
Covariance provides a measure of the strength of the correlation between two or more sets of random variates. The covariance for two random variates 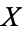 and
and 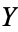 , each with sample size
, each with sample size 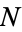 , is defined by the expectation value
, is defined by the expectation value
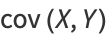 |
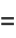 |
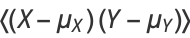 |
(1) |
 |
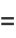 |
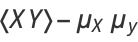 |
(2) |
where 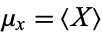 and
and 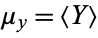 are the respective means, which can be written out explicitly as
are the respective means, which can be written out explicitly as
 |
(3) |
For uncorrelated variates,
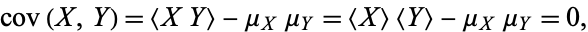 |
(4) |
so the covariance is zero. However, if the variables are correlated in some way, then their covariance will be nonzero. In fact, if 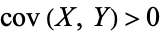 , then
, then 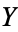 tends to increase as
tends to increase as 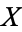 increases, and if
increases, and if 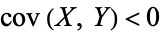 , then
, then 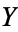 tends to decrease as
tends to decrease as 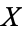 increases. Note that while statistically independent variables are always uncorrelated, the converse is not necessarily true.
increases. Note that while statistically independent variables are always uncorrelated, the converse is not necessarily true.
In the special case of 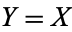 ,
,
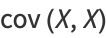 |
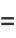 |
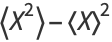 |
(5) |
 |
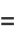 |
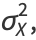 |
(6) |
so the covariance reduces to the usual variance 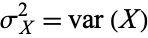 . This motivates the use of the symbol
. This motivates the use of the symbol 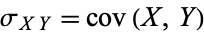 , which then provides a consistent way of denoting the variance as
, which then provides a consistent way of denoting the variance as 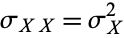 , where
, where 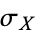 is the standard deviation.
is the standard deviation.
The derived quantity
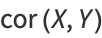 |
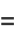 |
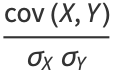 |
(7) |
 |
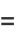 |
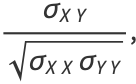 |
(8) |
is called statistical correlation of 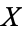 and
and 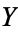 .
.
The covariance is especially useful when looking at the variance of the sum of two random variates, since
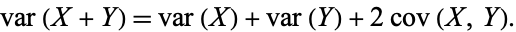 |
(9) |
The covariance is symmetric by definition since
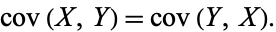 |
(10) |
Given 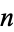 random variates denoted
random variates denoted 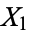 , ...,
, ..., 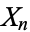 , the covariance
, the covariance 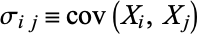 of
of 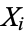 and
and 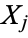 is defined by
is defined by
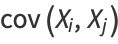 |
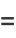 |
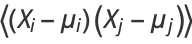 |
(11) |
 |
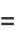 |
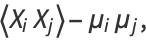 |
(12) |
where 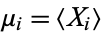 and
and 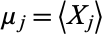 are the means of
are the means of 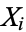 and
and 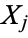 , respectively. The matrix
, respectively. The matrix 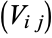 of the quantities
of the quantities 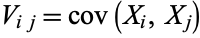 is called the covariance matrix.
is called the covariance matrix.
The covariance obeys the identities
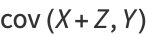 |
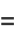 |
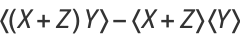 |
(13) |
 |
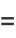 |
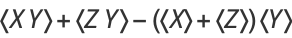 |
(14) |
 |
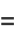 |
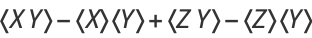 |
(15) |
 |
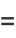 |
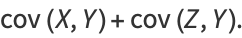 |
(16) |
By induction, it therefore follows that
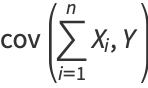 |
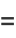 |
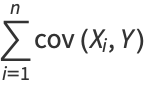 |
(17) |
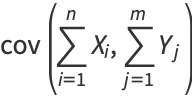 |
 |
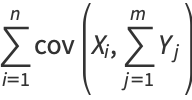 |
(18) |
 |
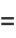 |
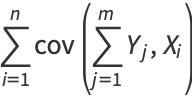 |
(19) |
 |
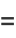 |
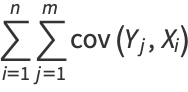 |
(20) |
 |
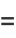 |
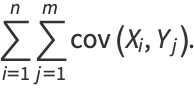 |
(21) |
REFERENCES:
Snedecor, G. W. and Cochran, W. G. Statistical Methods, 7th ed. Ames, IA: Iowa State Press, p. 180, 1980.
Spiegel, M. R. Theory and Problems of Probability and Statistics, 2nd ed. New York: McGraw-Hill, p. 298, 1992.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|