


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-5-2021
Date: 10-4-2021
Date: 24-4-2021
|
The Gini coefficient (or Gini ratio) 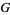 is a summary statistic of the Lorenz curve and a measure of inequality in a population. The Gini coefficient is most easily calculated from unordered size data as the "relative mean difference," i.e., the mean of the difference between every possible pair of individuals, divided by the mean size
is a summary statistic of the Lorenz curve and a measure of inequality in a population. The Gini coefficient is most easily calculated from unordered size data as the "relative mean difference," i.e., the mean of the difference between every possible pair of individuals, divided by the mean size 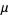 ,
,
 |
(Dixon et al. 1987, Damgaard and Weiner 2000). Alternatively, if the data is ordered by increasing size of individuals, 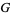 is given by
is given by
 |
(Dixon et al. 1988, Damgaard and Weiner 2000), correcting the typographical error in the denominator given in the original paper (Dixon et al. 1987).
The Gini coefficient ranges from a minimum value of zero, when all individuals are equal, to a theoretical maximum of one in an infinite population in which every individual except one has a size of zero. It has been shown that the sample Gini coefficients defined above need to be multiplied by 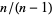 in order to become unbiased estimators for the population coefficients.
in order to become unbiased estimators for the population coefficients.
REFERENCES:
Damgaard, C. and Weiner, J. "Describing Inequality in Plant Size or Fecundity." Ecology 81, 1139-1142, 2000.
Dixon, P. M.; Weiner, J.; Mitchell-Olds, T.; and Woodley, R. "Bootstrapping the Gini Coefficient of Inequality." Ecology 68, 1548-1551, 1987.
Dixon, P. M.; Weiner, J.; Mitchell-Olds, T.; and Woodley, R. "Erratum to 'Bootstrapping the Gini Coefficient of Inequality.' " Ecology 69, 1307, 1988.
Gini, C. "Variabilitá e mutabilita." 1912. Reprinted in Memorie di metodologia statistica (Ed. E. Pizetti and T. Salvemini.) Rome: Libreria Eredi Virgilio Veschi, 1955.
Glasser, G. J. "Variance Formulas for the Mean Difference and Coefficient of Concentration." J. Amer. Stat. Assoc. 57, 648-654, 1962.
Sen, A. On Economic Inequality. Oxford, England: Clarendon Press, 1973.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
وفد كلية الزراعة في جامعة كربلاء يشيد بمشروع الحزام الأخضر
|
|
|