Liouville Number

A Liouville number is a transcendental number which has very close rational number approximations. An irrational number 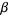 is called a Liouville number if, for each 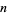, there exist integers  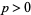and 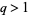 such that

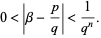Note that the first inequality is true by definition, since it follows immediately from the fact that 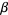 is irrational and hence cannot be equal to  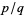for any values of  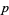and .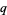

Liouville's constant is an example of a Liouville number and is sometimes called "the" Liouville number or "Liouville's number" (Wells 1986, p. 26). Mahler (1953) proved that 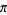 is not a Liouville number.

REFERENCES:

Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 147, 1997.

Mahler, K. "On the Approximation of 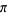." Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.