الاطياف الجزيئية Molecular Spectra

تملك الجزيئة طاقة دورانية E_r وطاقة اهتزازية E_v بالاضافة الى الطاقة الالكترونية. الطاقة الدورانية تاتي من دوران الجزيئة حول محور او عدة محاور والطاقة الاهتزازية تأتي من إهتزاز ذرات الجزيئة حول مواقع اتزانها مثل اهتزاز كتلتين نطقيتين مرتبطتين بنهايتي نابض حلزوني كتلته مهملة والاصرة بين النواتين التي تمسك الذرتين سوية في الجزيئة مرنة والذرتان تهتزان حول موقع اتزانهما بثابت قوة مكافئ k وعندما تتمدد الاصرة او تتقلص فان الطاقة الاهتزازية E_v تتناوب بين طاقة كامنة وطاقة حركية ومقدارالطاقة الكامنة المخزونة في النابض يساوي ½ k x² عندما يتمدد او يتقلص النابض بمسافة مقدارها x عن موقع اتزانه، بالنسبة للجزيئة عن طول الاصرة r₀. ان تردد الاهتزاز الطبيعي لجزيئة ثنائية الذرة تهتز ذراتها كمتذبذب توافقي بسيط يساوي 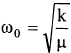حيث μ الكتلة المختزلة للذرتين المهتزتين وزمن الذبذبة الواحدة يساوي . يجب تزويد الجزيئة بالطاقة لتفكيكها الى ذرات لذلك الطاقة الكلية للجزيئة E_t تكون سالبة ولان طاقة الاهتزازات الجزيئية موجبة فان الطاقة الكلية للجزيئة تقل عندما تهتز ذرات الجزيئة، واذا اهتزت الذرات بطاقة كبيرة فقد تصبح اكبر من الطاقة الكلية للجزيئة وتتفكك الجزيئة الى ذرات منفصلة. تقع الذرات في الجزيئة في بئر جهد U بشكل قطع مكافئ parabola U=1/2kx² وطاقات الاهتزاز المسموحة E(v) في هذا البئر وفقا لميكانيكا الكم تعطى

بالمعادلة (E(v) = hω₀(v+1/2 حيث v=0,1,2,…. وقيمة v=0 وهي الحالة الارضية، حالة الطاقة الاعلى مباشرة فوق الطاقة الارضية E₀ = 1/2 hω₀ للعدد الكمي الاهتزازي v = 1 والاهتزازات محصورة اساسا داخل بئر الجهد (منحني القطع المكافئ المرسوم بالنقاط في شكل 1) ولكن الدوال الموجية تمتد خارج بئر الجهد لتسمح باحتمالية ضعيفة لتواجد الذرات خارج حدود الجهد وفقا للنظرية الكمية.​

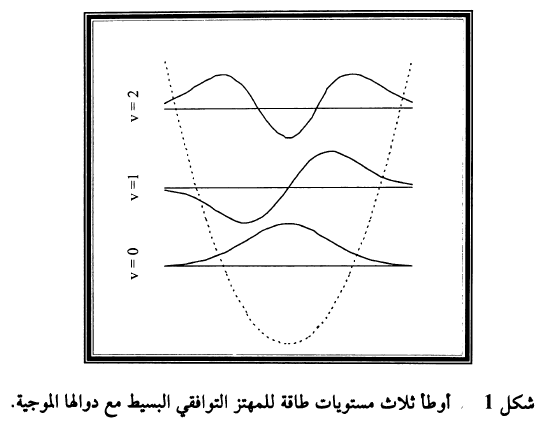
انطلاقا من مبدأ اللاتاكيد في موقع الذرة توجد احتمالية قليلة لاختراق الذرة لحاجز الجهد وعبورها لحدوده بعد مرور زمن كاف وتدعى عملية عبور حاجز الجهد بظاهرة النفق tunneling. ان الجزيئة تبقى تهتز بطاقة hω₀​1/2 ولا يمكن ايقاف اهتزازها وفقا لمبدأ اللاتأكيد uncertainty principle في النظرية الكمية فحتى في درجة حرارة الصفر المطلق توجد حركة اهتزازية جزيئية.

وتخضع حركة الجزيئة الدورانية لقوانين ميكانيكا الكم وتاخذ طاقة الجزيئة الدورانية قيما محددة يمكن فقط ايجادها من المعادلة: E(J)=h²/2I J(J+1) حيث I عزم القصور الدوراني للجزيئة حول محمور عمودي على الخط الواصل بين الذرتين.

وتبعد مستويات الطاقة الالكترونية عن بعضها بفرق طاقة بضعة الكترون فولت، بينما مستويات الطاقة الاهتزازية تبعد عن بعضها بفرق طاقة ΔE_v بحدود اعشار الالكترون فولت وفرق الطاقة (ΔE(J للمستويات الدورانية بحدود 10^-3 الى 10^-2 الكترون فولت.

تحدث الانتقالات الالكترونية بين مستويات الطاقة الالكترونية عندما يمتص او يبعث الالكترون طاقة في مدى الضوء المرئي من طيف الاشعاع الكهرومغناطيسي، بينما الانتقالات بين مستويات الطاقة الاهتزازية تعود تردداتها الى طيف تحت الحمراء، والانتقالات الدورانية تكون في مدى طيف الموجات الدقيقة وموجات الراديو.

يتكون الطيف الجزيئي الناتج من الانتقالات السابقة الذكر من حزم (طيف حزمة (band spectrum لان كل حالة الكترونية لها تركيب دقيق fine structure، والمستويات الدقيقة منتظمة بشكل عام وتتكون كل حزمة من عدة خطوط متقاربة كما تظهر في جهاز المطياف. لكل جزيئة طيفها الخاص بها ويمكن التعرف على الجزيئة من خلال طيفها.

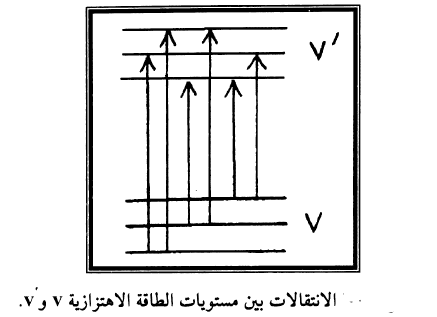
عندما يحصل تغير في الحالة الالكترونية من الحالة الالكترونية للجزيئة من الحالة n الى الحالة "n ووفقا لقواعد اختيار الانتقالات يتغير العدد الكمي الاهتزازي v والعدد الدوراني j. لتغير معين في العدد الكمي الالكتروني nΔ توجد عدة خطوط تعود الى تغيرات دورانية مختلفة في العدد الكمي الدوراني j. يبين شكل (2) حزمة اهتزازية مع الانتقالات المسموح بها بين مستويات الطاقة للعددين الكميين v و'v.

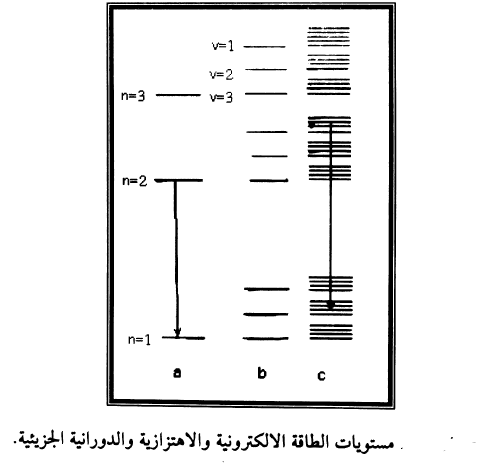
يكون للجزيئة التي تحصل على طاقة من مصدر خارجي قيم مختلفة للطاقة الكلية اعتمادا على ان التغير يحصل في الحالة الالكترونية فقط ام تحصل في الحالات الاهتزازية والدورانية ايضا. في شكل (3) مبين مستويات الطاقة الجزيئية. في a تغيرات في مستويات الطاقة الالكترونية فقط. لطاقة الالكترونية معينة فان الجزيئة يمكن ان تتحرك حركة اهتزازية ايضا، لذلك فان كل مستوى طاقة الكتروني يحتوي على مستويات طاقة اهتزازية بمقدار E_v في b. واخيرا فان الجزيئات التي لها نفس الطاقة الالكترونية والطاقة الاهتزازية قد يكون لها طاقة دورانية مختلفة فكل مستوى طاقة اهتزازي يحتوي على عدد من مستويات الطاقة الدروانية c والتي تقع فوق E_v بمقدار طاقة المستوى الدوراني E_r.

شكل (2)

شكل (3)

الاشعاع الكهرومغناطيسي المنبعث من جزيئة قد يكون مصدره طاقة الجزيئة الالكترونية، الاهتزازية، الدورانية، او كل هذه الطاقة سوية وتتكون طاقة فوتون الاشعاع الكهرومغناطيسي المنبعث من جزيئة hv من الحدود الآتية:

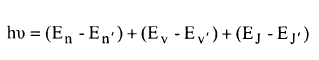
حيث 'J', v', n تشير الى الحالة النهائية. لذلك تبعث الجزيئة طيفا يتكون من عدد كبير جدا من الخطوط المنتظمة الترتيب. كل الخطوط الطيفية العائدة الى الحد الاول من طاقة الفوتون المنبعث ولكن لقيم مختلفة من الحد الثالث تشكل حزمة واحدة وتتراكم خطوط كل حزمة في اتجاه نهاية الحزمة مكونة راس الحزمة. الحزم المختلفة تعود الى القيمة نفسها E_nΔ ولكن لقيم مختلفة من E_vΔ.

ولا يظهر الانتظار في ترتيب خطوط الحزمة فقط، ولكن في ترتيب الحزم نفسها ايضا. فالحزم العائدة للقيمة نفسها E_v ولكن لقيم مختلفة 'Ev تشكل مجموع حزم حيث مقدار الفاصل بين حزمتين متتاليتين يصبح اصغر فاصغر باتجاه تقليل الطول الموجي λ. اعتمادا على قيمة E_nΔ توجد مجموعات مختلفة وكلها تشبه بعضها البعض ولكن مع ازاحة ويدعى نظام مجموعات الحزم الذي يظهر عندما لا يوجد تغير في الطاقة الالكترونية ولكن التغير يكون في الطاقة الاهتزازية والطاقة الدورانية بالطيف الاهتزازي – الدوراني. كما مبين في شكل (3) فان الفرق في طاقة المستويات الاهتزازية ومستويات الطاقة الدورانية قليل ذلك تقع خطوط الطيف الاهتزازي والدوراني في مدى طيف الاشعة تحت الحمراء.

وفي ظاهرة رامان Raman يمكن ايجاد مقدار مستويات الطاقة الاهتزازية E_v ومقدار مستويات الطاقة الدورانية E_r للجزيئات وكذلك بحث تركيبها فعند اضاءة مادة شفافة بضوء احادي اللون فان تحليل الضوء المستطار من قبل الجزيئة بمطياف يبين وجود خطوط طيفية على جانبي خط الضوء الاحادي اللون الساقط على الجزيئة والتي تدعى خط رايلي Rayliegh line. ظاهرة رامان يفسرها ميكانيكا الكم بتبادل الطاقة بين الجزيئة والضوء الساقط عليها و ينقل فوتون الضوء المستطار من قبل الجزيئة جزء من طاقته EΔ. الى الجزيئة وهذه الطاقة تذهب الى زيادة طاقة الجزيئة الاهتزازية والدورانية لذلك فان الفوتون المستطار تقل طاقته بمقدار ΔE ويظهر خط طيفي جديد، خط ستوك stoke line ، لم يكن موجوداً قبل الاستطارة وتردده 'v اقل من تردد الفوتون الساقط v. معادلة الطاقة في هذه الحالة هي: hv' = hv - ΔE. ويمكن ان يظهر خط آخر تردده اعلى من تردد الفوتون الساقط، خط ضد ستوك anti-Stoke line، عندما تنتقل طاقة الجزيئة الاهتزازية والدورانية الى الفوتون الساقط. ومعادلة الطاقة في هذه الحالة هي: hv' = hv + ΔE.

ان تحليل الطيف الجزيئي يعطي معلومات كثيرة عن الجزيئة فمن دراسة الاطياف الجزيئية يمكن معرفة التركيب الجزيئي لوجود علاقة متبادلة بين مستويات الطاقة وبئر الجهد ومن الاطياف الدورانية يمكن الحصول على التركيب الهندسي للجزيئة، الاطياف الاهتزازية تعطي معلومات عن القوى بين الذرات المهتزة في الجزية، والاطياف الالكترونية تجهزنا بمعلومات عن الحالات الالكترونية، استقرارية الحالات الالكترونية، وتوزيع الكتروناتها وعرض الخط الطيفي يزودنا بمعلومات عن حالات الطاقة فوق الحالة الارضية وعن طاقة تفكك الجزيئة.