


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-10-2019
Date: 30-12-2019
Date: 10-2-2020
|
Three types of 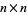 matrices can be obtained by writing Pascal's triangle as a lower triangular matrix and truncating appropriately: a symmetric matrix
matrices can be obtained by writing Pascal's triangle as a lower triangular matrix and truncating appropriately: a symmetric matrix 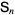 with
with 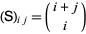 , a lower triangular matrix
, a lower triangular matrix 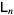 with
with 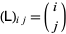 , and an upper triangular matrix
, and an upper triangular matrix 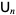 with
with 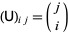 , where
, where 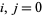 , 1, ...,
, 1, ..., 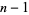 . For example, for
. For example, for 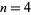 , these would be given by
, these would be given by
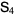 |
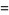 |
![[1 1 1 1; 1 2 3 4; 1 3 6 10; 1 4 10 20]](https://mathworld.wolfram.com/images/equations/PascalMatrix/Inline13.gif) |
(1) |
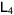 |
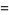 |
![[1 ; 1 1 ; 1 2 1 ; 1 3 3 1]](https://mathworld.wolfram.com/images/equations/PascalMatrix/Inline16.gif) |
(2) |
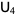 |
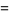 |
![[1 1 1 1; 1 2 3; 1 3; 1].](https://mathworld.wolfram.com/images/equations/PascalMatrix/Inline19.gif) |
(3) |
The Pascal 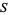 -matrix or order
-matrix or order 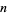 is implemented in the Wolfram Language as LinearAlgebra`PascalMatrix[n].
is implemented in the Wolfram Language as LinearAlgebra`PascalMatrix[n].
These matrices have some amazing properties. In particular, their determinants are all equal to 1
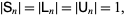 |
(4) |
and
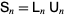 |
(5) |
(Edelman and Strang).
Edelman and Strang give four proofs of the identity (5), the most straightforward of which is
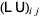 |
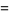 |
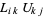 |
(6) |
 |
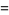 |
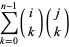 |
(7) |
 |
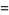 |
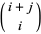 |
(8) |
 |
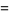 |
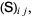 |
(9) |
where Einstein summation has been used.
REFERENCES:
Abbott, P. "Tricks of the Trade: Pascal Matrices." Mathematica J. 9, 691-694, 2005.
Edelman, A. and Strang, G. "Pascal Matrices." http://web.mit.edu/18.06/www/pascal-work.pdf.
Strang, G. Introduction to Linear Algebra, 3rd ed. Wellesley-Cambridge Press, 2003.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|