


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-10-2020
Date: 21-12-2020
Date: 7-6-2020
|

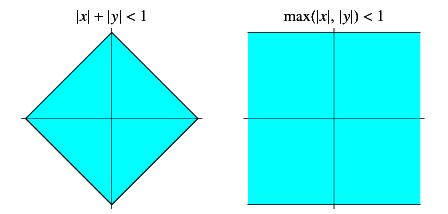
The term "square" can be used to mean either a square number ("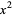 is the square of
is the square of  ") or a geometric figure consisting of a convex quadrilateral with sides of equal length that are positioned at right angles to each other as illustrated above. In other words, a square is a regular polygon with four sides.
") or a geometric figure consisting of a convex quadrilateral with sides of equal length that are positioned at right angles to each other as illustrated above. In other words, a square is a regular polygon with four sides.
When used as a symbol, 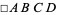 denotes a square geometric figure with given vertices, while
denotes a square geometric figure with given vertices, while 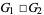 is sometimes used to denote a graph product (Clark and Suen 2000).
is sometimes used to denote a graph product (Clark and Suen 2000).
A square is a special case of an isosceles trapezoid, kite, parallelogram, quadrilateral, rectangle, rhombus, and trapezoid.
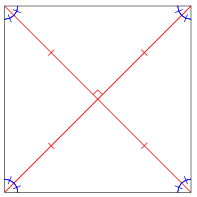
The diagonals of a square bisect one another and are perpendicular (illustrated in red in the figure above). In addition, they bisect each pair of opposite angles (illustrated in blue).
The perimeter of a square with side length 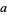 is
is
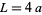 |
(1) |
and the area is
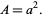 |
(2) |
The inradius 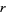 , circumradius
, circumradius 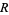 , and area
, and area 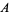 can be computed directly from the formulas for a general regular polygon with side length
can be computed directly from the formulas for a general regular polygon with side length 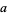 and
and 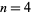 sides,
sides,
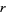 |
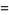 |
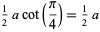 |
(3) |
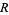 |
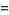 |
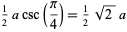 |
(4) |
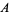 |
 |
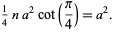 |
(5) |
The length of the polygon diagonal of the unit square is 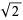 , sometimes known as Pythagoras's constant.
, sometimes known as Pythagoras's constant.
The equation
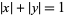 |
(6) |
gives a square of circumradius 1, while
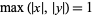 |
(7) |
gives a square of circumradius 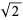 .
.
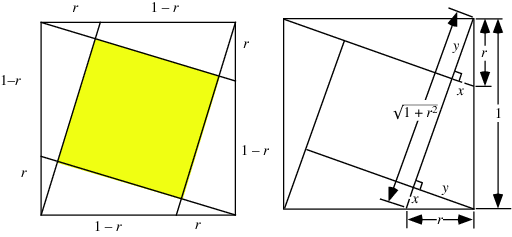
The area of a square constructed inside a unit square as shown in the above diagram can be found as follows. Label  and
and 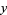 as shown, then
as shown, then
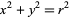 |
(8) |
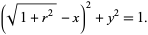 |
(9) |
Plugging (8) into (9) gives
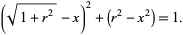 |
(10) |
Expanding
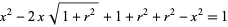 |
(11) |
and solving for  gives
gives
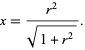 |
(12) |
Plugging in for 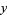 yields
yields
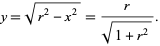 |
(13) |
The area of the shaded square is then
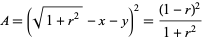 |
(14) |
(Detemple and Harold 1996).
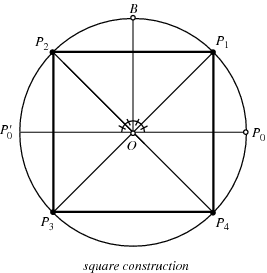
The straightedge and compass construction of the square is simple. Draw the line  and construct a circle having
and construct a circle having  as a radius. Then construct the perpendicular
as a radius. Then construct the perpendicular  through
through  . Bisect
. Bisect 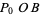 and
and  to locate
to locate 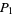 and
and 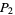 , where
, where  is opposite
is opposite 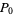 . Similarly, construct
. Similarly, construct 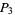 and
and 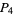 on the other semicircle. Connecting
on the other semicircle. Connecting 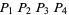 then gives a square.
then gives a square.
An infinity of points in the interior of a square are known whose distances from three of the corners of a square are rational numbers. Calling the distances 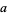 ,
, 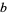 , and
, and 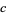 where
where 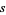 is the side length of the square, these solutions satisfy
is the side length of the square, these solutions satisfy
 |
(15) |
(Guy 1994). In this problem, one of 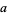 ,
, 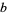 ,
, 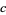 , and
, and 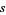 is divisible by 3, one by 4, and one by 5. It is not known if there are points having distances from all four corners rational, but such a solution requires the additional condition
is divisible by 3, one by 4, and one by 5. It is not known if there are points having distances from all four corners rational, but such a solution requires the additional condition
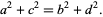 |
(16) |
In this problem, 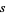 is divisible by 4 and
is divisible by 4 and 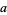 ,
,  ,
, 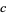 , and
, and 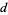 are odd. If
are odd. If 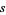 is not divisible by 3 (5), then two of
is not divisible by 3 (5), then two of 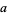 ,
, 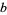 ,
, 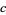 , and
, and 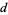 are divisible by 3 (5) (Guy 1994).
are divisible by 3 (5) (Guy 1994).
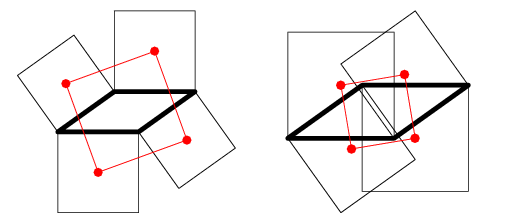
The centers of four squares erected either internally or externally on the sides of a parallelograms are the vertices of a square (Yaglom 1962, pp. 96-97; Coxeter and Greitzer 1967, p. 84).
REFERENCES:
Clark, W. E. and Suen, S. "An Inequality Related to Vizing's Conjecture." Electronic J. Combinatorics 7, No. 1, N4, 1-3, 2000. https://www.combinatorics.org/Volume_7/Abstracts/v7i1n4.html.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., p. 84, 1967.
Detemple, D. and Harold, S. "A Round-Up of Square Problems." Math. Mag. 69, 15-27, 1996.
Dixon, R. Mathographics. New York: Dover, p. 16, 1991.
Eppstein, D. "Rectilinear Geometry." https://www.ics.uci.edu/~eppstein/junkyard/rect.html.
Fischer, G. (Ed.). Plate 1 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, p. 2, 1986.
Fukagawa, H. and Pedoe, D. "One or Two Circles and Squares," "Three Circles and Squares," and "Many Circles and Squares (Casey's Theorem)." §3.1-3.3 in Japanese Temple Geometry Problems. Winnipeg, Manitoba, Canada: Charles Babbage Research Foundation, pp. 37-42 and 117-125, 1989.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 165 and 167, 1984.
Guy, R. K. "Rational Distances from the Corners of a Square." §D19 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 181-185, 1994.
Harris, J. W. and Stocker, H. "Square." §3.6.6 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, pp. 84-85, 1998.
Kern, W. F. and Bland, J. R. Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 2, 1948.
Yaglom, I. M. Geometric Transformations I. New York: Random House, pp. 96-97, 1962.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|