


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-8-2020
Date: 2-5-2020
Date: 24-9-2020
|
A number which is simultaneously octagonal and square. Let 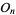 denote the
denote the 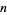 th octagonal number and
th octagonal number and 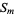 the
the 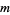 th square number, then a number which is both octagonal and square satisfies the equation
th square number, then a number which is both octagonal and square satisfies the equation 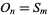 , or
, or
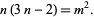 |
(1) |
Completing the square and rearranging gives
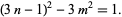 |
(2) |
Therefore, defining
 |
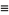 |
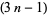 |
(3) |
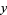 |
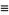 |
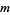 |
(4) |
gives the Pell equation
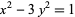 |
(5) |
The first few solutions are 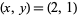 , (7, 4), (26, 15), (97, 56), (362, 209), (1351, 780), .... These give the solutions
, (7, 4), (26, 15), (97, 56), (362, 209), (1351, 780), .... These give the solutions 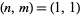 , (8/3, 4), (9, 15), (98/3, 56), (121, 209), ..., of which the integer solutions are (1, 1), (9, 15), (121, 209), (1681, 2911), ... (OEIS A046184 and A028230), corresponding to the octagonal square numbers 1, 225, 43681, 8473921, 1643897025, ... (OEIS A036428).
, (8/3, 4), (9, 15), (98/3, 56), (121, 209), ..., of which the integer solutions are (1, 1), (9, 15), (121, 209), (1681, 2911), ... (OEIS A046184 and A028230), corresponding to the octagonal square numbers 1, 225, 43681, 8473921, 1643897025, ... (OEIS A036428).
REFERENCES:
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, p. 329, 1990.
Konhauser, J. D. E.; Velleman, D.; and Wagon, S. Which Way Did the Bicycle Go? And Other Intriguing Mathematical Mysteries. Washington, DC: Math. Assoc. Amer., p. 104, 1996.
Sloane, N. J. A. Sequences A028230, A036428, and A046184 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|