Scholz Conjecture

Let the minimal length of an addition chain for a number 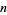 be denoted 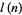. Then the Scholz conjecture, also called the Scholz-Brauer conjecture or Brauer-Scholz conjecture, states that

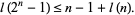The conjecture has been proven for a variety of special cases but not in general.

REFERENCES:

Brauer, A. T. "On Addition Chains." Bull. Amer. Math. Soc. 45, 637-739, 1939.

Gioia, A. A. and Subbarao, M. V. "The Scholz-Brauer Problem in Addition Chains. II." Congr. Numer. 22, 251-274, 1978.

Gioia, A. A.; Subbarao, M. V.; and Sugunamma, M. "The Scholz-Brauer Problem in Addition Chains." Duke Math. J. 29, 481-487, 1962.

Guy, R. K. Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, p. 169, 2004.

Scholz, A. "Aufgabe 253." Jahresber. deutsche Math.-Verein. II 47, 41-42, 1937.

Utz, W. R. "A Note on the Scholz-Brauer Problem in Addition Chains." Proc. Amer. Math. Soc. 4, 462-463, 1953.