The Chebotarev density theorem is a complicated theorem in algebraic number theory which yields an asymptotic formula for the density of prime ideals of a number field 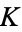 that split in a certain way in an algebraic extension  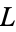of 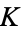. When the base field is the field  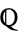of rational numbers, the theorem becomes much simpler.

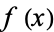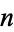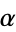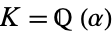Let  be a monic irreducible polynomial of degree  with integer coefficients with root , let , let 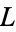 be the normal closure of 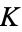, and let  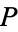be a partition  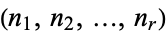of 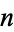, i.e., an ordered set of positive integers  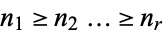with 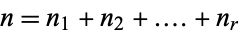. A prime is said to be unramified (over the number field 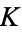) if it does not divide the discriminant of 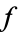. Let 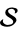 denote the set of unramified primes. Consider the set  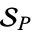of unramified primes for which  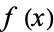factors as  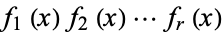modulo 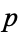, where  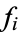is irreducible modulo  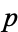and has degree 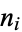. Also define the density  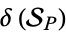of primes in  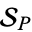as follows:

{p in S_P:p<=N})/(#{p in S:p<=N}). " src="http://mathworld.wolfram.com/images/equations/ChebotarevDensityTheorem/NumberedEquation1.gif" style="height:38px; width:192px" />

Now consider the Galois group 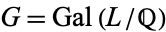 of the number field 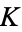. Since this is a subgroup of the symmetric group 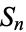, every element of  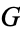can be represented as a permutation of  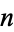letters, which in turn has a unique representation as a product of disjoint cycles. Now consider the set of elements  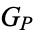of 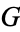 consisting of disjoint cycles of length 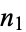, , 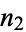..., 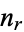. Then .

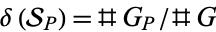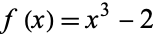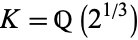As an example, let , so  and 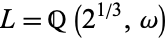, where  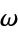is a primitive root of unity. Since  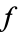has discriminant 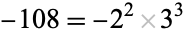, the only ramified primes are 2 and 3.

Let 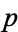 be an unramified prime. Then  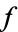has a root (mod 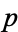) if and only if 2 has a cube root (mod 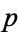), which occurs whenever  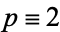(mod 3) or  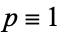(mod 3) and 2 has multiplicative order modulo  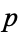dividing 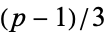. The first case occurs for half of all unramified primes and the second case occurs for one sixth of all primes. In the first case, 2 has a unique cube root modul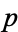o , so 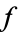 factors as the product of a linear and an irreducible quadratic factor mod 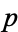. In the second case, 2 has three distinct cube roots mod 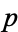, so 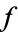 has three linear factors mod 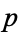. In the remaining case, which occurs for 1/3 of all unramified primes,  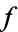is irreducible mod 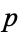. Now consider the corresponding elements of 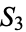. The first case corresponds to products of 2-cycles and 1-cycles (the identity), of which there are three, or half of the elements of 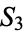, the second case corresponds to products of three 1-cycles, or the identity, of which there is just one element, or one sixth of the elements of 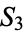, and the remaining case corresponds to 3-cycles, of which there are two, or one third the elements of 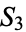. Since  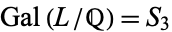in this case, the Chebotarev density theorem holds for this example.

The Chebotarev density theorem can often be used to determine the Galois group of a given irreducible polynomial 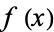 of degree 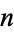. To do so, count the number of unramified primes up to a specified bound for which  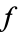factors in a certain way and then compare the results with the fractions of elements of each of the transitive subgroups of  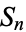with the same cyclic structure. Lenstra provides some good examples of this procedure.

REFERENCES:

Lenstra, H. "The Chebotarev Density Theorem." http://websites.math.leidenuniv.nl/algebra/Lenstra-Chebotarev.pdf.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد