Power Fractional Parts

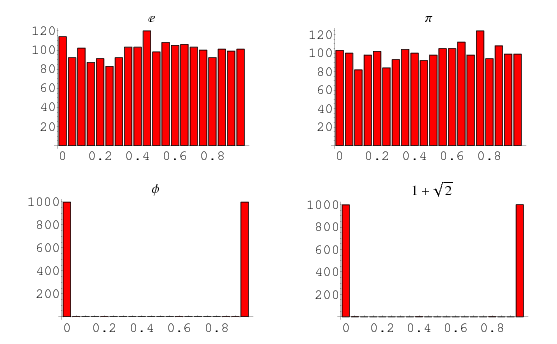
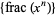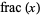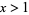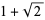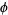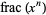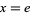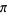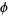Hardy and Littlewood (1914) proved that the sequence , where  is the fractional part, is equidistributed for almost all real numbers  (i.e., the exceptional set has Lebesgue measure zero). Exceptional numbers include the positive integers, the silver ratio  (Finch 2003), and the golden ratio . The plots above illustrate the distribution of  for , , , and 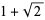. Candidate members of the measure one set are easy to find, but difficult to prove. However, Levin has explicitly constructed such an example (Drmota and Tichy 1997).

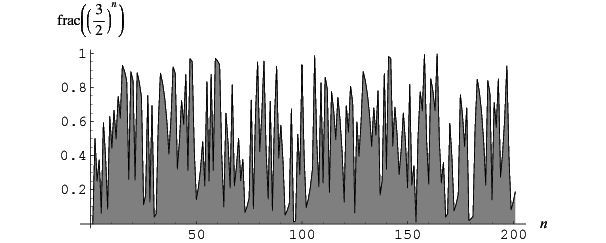
The properties of 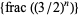, the simplest such sequence for a rational number 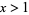, have been extensively studied (Finch 2003). The first few terms are 0, 1/2, 1/4, 3/8, 1/16, 19/32, 25/64, 11/128, 161/256, 227/512, ... (OEIS A002380 and A000079; Pillai 1936; Lehmer 1941), plotted above (Wolfram 2002, pp. 121-122). For example,  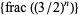has infinitely many accumulation points in both  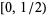and  (Pisot 1938, Vijayaraghavan 1941). Furthermore, Flatto et al. (1995) proved that any subinterval of  containing all but at most finitely many accumulation points of 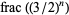 must have length at least 1/3. Surprisingly, the sequence  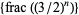is also connected with the Collatz problem and with Waring's problem.

Numbers of the form 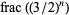, where  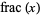is the fractional part, appear in Waring's problem. In particular, Waring's problem can be solved completely if the inequality

holds. No counterexample to this inequality is known, and it is even believed that it can be extended to

for 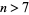 (Bennett 1993, 1994; Finch 2003). Furthermore, the constant 3/4 can be decreased to 0.5769 (Beukers 1981, Dubitskas 1990). Unfortunately, these inequalities have not been proved.

REFERENCES:

Bennett, M. A. "Fractional Parts of Powers of Rational Numbers." Math. Proc. Cambridge Philos. Soc. 114, 191-201, 1993.

Bennett, M. A. "An Ideal Waring Problem with Restricted Summands." Acta Arith. 66, 125-132, 1994.

Beukers, F. "Fractional Parts of Powers of Rational Numbers." Math. Proc. Cambridge Philos. Soc. 90, 13-20, 1981.

Drmota, M. and Tichy, R. F. Sequences, Discrepancies and Applications. New York: Springer-Verlag, 1997.

Dubitskas, A. K. "A Lower Bound for the Quantity 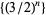." Russian Math. Survey 45, 163-164, 1990.

Finch, S. R. "Powers of 3/2 Modulo One." §2.30.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 194-199, 2003.

Flatto, L.; Lagarias, J. C.; Pollington, A. D. "On the Range of Fractional Parts 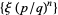." Acta Arith. 70, 125-147, 1995.

Hardy, G. H. and Littlewood, J. E. "Some Problems of Diophantine Approximation." Acta Math. 37, 193-239, 1914.

Lehmer, D. H. Guide to Tables in the Theory of Numbers. Bulletin No. 105. Washington, DC: National Research Council, p. 82, 1941.

Pillai, S. S. "On Waring's Problem." J. Indian Math. Soc. 2, 16-44, 1936.

Pisot, C. "La répartition modulo 1 et les nombres algébriques." Annali di Pisa 7, 205-248, 1938.

Sloane, N. J. A. Sequences A000079/M1129 and A002380/M2235 in "The On-Line Encyclopedia of Integer Sequences."

Vijayaraghavan, T. "On the Fractional Parts of the Powers of a Number (I)." J. London Math. Soc. 15, 159-160, 1940.

Vijayaraghavan, T. "On the Fractional Parts of the Powers of a Number (II)." Proc. Cambridge Phil. Soc. 37, 349-357, 1941.

Vijayaraghavan, T. "On the Fractional Parts of the Powers of a Number (III)." J. London Math. Soc. 17, 137-138, 1942.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 121-122, 2002.