الطرق التقريبية لحساب الدوال الموجية الالكترونية: تقريب LCAO

بما ان الحالة الالكترونية لجزيئة ثنائية الذرة تتعين بحالات الذرات المنفصلة فان الاختيار الواضح للدالة الاختيارية Φ في المعادلة الاتية:

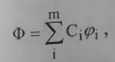......(i) 

هو الجمع الخطي للدوال الذاتية Φ_{A و} Φ_B لهذه الحالات الذرية. هذا التقريب للدالة الموجية الجزيئية يدعى الجمع الخطي للمدارات الذرية Linear combination oِِِِِf atomic orbitals. اذا اخترنا لجزيئة ثنائية الذرة AB  الدالة Φ = C₁Φ_A + C₂Φ_B مع المدارات الذرية المعايرة  Φ_{A و} Φ_B بحيث ان Φ_A| Φ_A >= 1>  وكذلك Φ_B| Φ_B >= 1> فان دالة الموجة الجزيئية Φ يمكن معايرتها كالآتي:

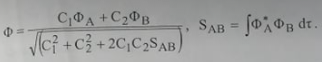...............(1)

افضل الدوال Φ يمكن ايجادها وفقا لمبدأ التغيير بتفاصيل القيمة المتوقعة:

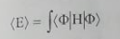................(2)

بالنسبة الى المكافئات C_i ومساواة النتيجة بالصفر، فنحصل على:

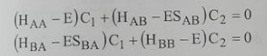................(3)

ومنها نصل الى:

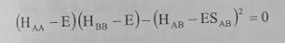................(4)

المعادلة (4) معادلة تربيعية للطاقة E ومنها نحصل على حلين (E₁(R و(E₂(R للطاقة. اذا كانت الذرتان متشابهتين وفي نفس الحالة الذرية (Φ_A = Φ​_B , H_AA = H_BB) نحصل الى التعبير:

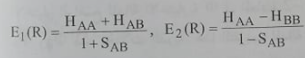....................(5)

في هذه الحالة المكافئتان C₁ وC₂  يمكن الحصول عليهما بتعويض المعادلة (3):

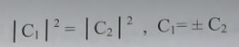................(6)

ان الجمع الخطي لمدارين ذريين متشابهين يفصل الطاقة الى مستويين E₁ وE₂. الفرق بين طاقة المستويين للحالة Φ_A = Φ​_B يعطي بالعلاقة:

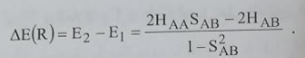...............(7)

يعتمد مقدار الفرق في الطاقة على قيمة تكامل التداخل S_AB, تكامل كولوم H_AA، وتكامل التبادل H_AB. التكاملات H_ik وS_ik تعطى بالعلاقة:

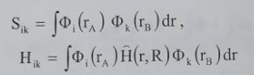.............(8) 

اخر الاخبار

اخبار العتبة العباسية المقدسة

أهالي كربلاء يحيون اليوم السابع لذكرى شهادة الإمام الحسين (عليه السلام)

مشروع أمير القراء الوطني يشهد مشاركة أكثر من 100 طالبٍ في مرحلته الثالثة

قسم الشؤون الفكرية يصدر دليلًا يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة

قسم الشؤون الفكرية يعلن عن توفير عددٍ من المكتبات الإلكترونية المتخصّصة للمؤسّسات الدينية والمكتبات العامّة

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon