


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2020
Date: 21-12-2020
Date: 12-12-2020
|
The number of ways a set of  elements can be partitioned into nonempty subsets is called a Bell number and is denoted
elements can be partitioned into nonempty subsets is called a Bell number and is denoted  (not to be confused with the Bernoulli number, which is also commonly denoted
(not to be confused with the Bernoulli number, which is also commonly denoted  ).
).
For example, there are five ways the numbers  can be partitioned:
can be partitioned:  ,
,  ,
,  ,
,  , and
, and  , so
, so  .
.
 , and the first few Bell numbers for
, and the first few Bell numbers for  , 2, ... are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, ... (OEIS A000110). The numbers of digits in
, 2, ... are 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, ... (OEIS A000110). The numbers of digits in  for
for  , 1, ... are given by 1, 6, 116, 1928, 27665, ... (OEIS A113015).
, 1, ... are given by 1, 6, 116, 1928, 27665, ... (OEIS A113015).
Bell numbers are implemented in the Wolfram Language as BellB[n].
Though Bell numbers have traditionally been attributed to E. T. Bell as a result of the general theory he developed in his 1934 paper (Bell 1934), the first systematic study of Bell numbers was made by Ramanujan in chapter 3 of his second notebook approximately 25-30 years prior to Bell's work (B. C. Berndt, pers. comm., Jan. 4 and 13, 2010).
The first few prime Bell numbers occur at indices  , 3, 7, 13, 42, 55, 2841, ... (OEIS A051130), with no others less than
, 3, 7, 13, 42, 55, 2841, ... (OEIS A051130), with no others less than  (Weisstein, Apr. 23, 2006). These correspond to the numbers 2, 5, 877, 27644437, ... (OEIS A051131).
(Weisstein, Apr. 23, 2006). These correspond to the numbers 2, 5, 877, 27644437, ... (OEIS A051131).  was proved prime by I. Larrosa Canestro in 2004 after 17 months of computation using the elliptic curve primality proving program PRIMO.
was proved prime by I. Larrosa Canestro in 2004 after 17 months of computation using the elliptic curve primality proving program PRIMO.
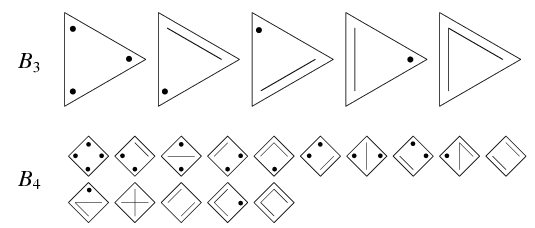
Bell numbers are closely related to Catalan numbers. The diagram above shows the constructions giving  and
and  , with line segments representing elements in the same subset and dots representing subsets containing a single element (Dickau). The integers
, with line segments representing elements in the same subset and dots representing subsets containing a single element (Dickau). The integers  can be defined by the sum
can be defined by the sum
 |
(1) |
where  is a Stirling number of the second kind, i.e., as the Stirling transform of the sequence 1, 1, 1, ....
is a Stirling number of the second kind, i.e., as the Stirling transform of the sequence 1, 1, 1, ....
The Bell numbers are given in terms of generalized hypergeometric functions by
 |
(2) |
(K. A. Penson, pers. comm., Jan. 14, 2007).
The Bell numbers can also be generated using the sum and recurrence relation
 |
(3) |
where  is a binomial coefficient, using the formula of Comtet (1974)
is a binomial coefficient, using the formula of Comtet (1974)
![B_n=[e^(-1)sum_(m=1)^(2n)(m^n)/(m!)]](https://mathworld.wolfram.com/images/equations/BellNumber/NumberedEquation4.gif) |
(4) |
for  , where
, where ![[x]](https://mathworld.wolfram.com/images/equations/BellNumber/Inline24.gif) denotes the ceiling function. Dobiński's formula gives the
denotes the ceiling function. Dobiński's formula gives the  th Bell number
th Bell number
 |
(5) |
A variation of Dobiński's formula gives
 |
 |
 |
(6) |
 |
 |
 |
(7) |
where  is a subfactorial (Pitman 1997).
is a subfactorial (Pitman 1997).
A double sum is given by
 |
(8) |
The Bell numbers are given by the generating function
 |
 |
 |
(9) |
 |
 |
 |
(10) |
 |
 |
 |
(11) |
 |
 |
![((-1)^(1/x)[xGamma(1-x^(-1))+Gamma(-x^(-1),-1)])/(ex)](https://mathworld.wolfram.com/images/equations/BellNumber/Inline44.gif) |
(12) |
 |
 |
 |
(13) |
 |
 |
 |
(14) |
and the exponential generating function
 |
(15) |
An amazing integral representation for  was given by Cesàro (1885),
was given by Cesàro (1885),
 |
 |
![(2n!)/(pie)I[int_0^pie^(e^(e^(ntheta)))sin(ntheta)dtheta]](https://mathworld.wolfram.com/images/equations/BellNumber/Inline54.gif) |
(16) |
 |
 |
![(2n!)/(pie)int_0^pie^(e^(costheta)cos(sint))sin[e^(costheta)sin(sintheta)]sin(ntheta)dtheta](https://mathworld.wolfram.com/images/equations/BellNumber/Inline57.gif) |
(17) |
(Becker and Browne 1941, Callan 2005), where ![I[z]](https://mathworld.wolfram.com/images/equations/BellNumber/Inline58.gif) denotes the imaginary part of
denotes the imaginary part of  .
.
The Bell number  is also equal to
is also equal to  , where
, where  is a Bell polynomial.
is a Bell polynomial.
de Bruijn (1981) gave the asymptotic formula
![(lnB_n)/n=lnn-lnlnn-1+(lnlnn)/(lnn)+1/(lnn)+1/2((lnlnn)/(lnn))^2+O[(lnlnn)/((lnn)^2)].](https://mathworld.wolfram.com/images/equations/BellNumber/NumberedEquation8.gif) |
(18) |
Lovász (1993) showed that this formula gives the asymptotic limit
![B_n∼n^(-1/2)[lambda(n)]^(n+1/2)e^(lambda(n)-n-1),](https://mathworld.wolfram.com/images/equations/BellNumber/NumberedEquation9.gif) |
(19) |
where  is given by
is given by
 |
(20) |
with  the Lambert W-function (Graham et al. 1994, p. 493). Odlyzko (1995) gave
the Lambert W-function (Graham et al. 1994, p. 493). Odlyzko (1995) gave
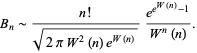 |
(21) |
Touchard's congruence states
 |
(22) |
when  is prime. This gives as a special case for
is prime. This gives as a special case for  the congruence
the congruence
 |
(23) |
for  prime. It has been conjectured that
prime. It has been conjectured that
 |
(24) |
gives the minimum period of  (mod
(mod  ). The sequence of Bell numbers
). The sequence of Bell numbers  is periodic (Levine and Dalton 1962, Lunnon et al. 1979) with periods for moduli
is periodic (Levine and Dalton 1962, Lunnon et al. 1979) with periods for moduli  , 2, ... given by 1, 3, 13, 12, 781, 39, 137257, 24, 39, 2343, 28531167061, 156, ... (OEIS A054767).
, 2, ... given by 1, 3, 13, 12, 781, 39, 137257, 24, 39, 2343, 28531167061, 156, ... (OEIS A054767).
The Bell numbers also have the curious property that
 |
 |
 |
(25) |
 |
 |
 |
(26) |
(Lenard 1992), where the product is simply a superfactorial and  is a Barnes G-function, the first few of which for
is a Barnes G-function, the first few of which for  , 1, 2, ... are 1, 1, 2, 12, 288, 34560, 24883200, ... (OEIS A000178).
, 1, 2, ... are 1, 1, 2, 12, 288, 34560, 24883200, ... (OEIS A000178).
REFERENCES:
Becker, H. W. and Browne, D. E. "Problem E461 and Solution." Amer. Math. Monthly 48, 701-703, 1941.
Bell, E. T. "Exponential Numbers." Amer. Math. Monthly 41, 411-419, 1934.
Blasiak, P.; Penson, K. A.; and Solomon, A. I. "Dobiński-Type Relations and the Log-Normal Distribution." J. Phys. A: Math. Gen. 36, L273-278, 2003.
Callan, D. "Cesàro's integral formula for the Bell numbers (corrected)." Oct. 3, 2005. https://www.stat.wisc.edu/~callan/papersother/cesaro/cesaro.pdf.
Cesàro, M. E. "Sur une équation aux différences mêlées." Nouv. Ann. Math. 4, 36-40, 1885.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, 1974.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 91-94, 1996.
de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 102-109, 1981.
Dickau, R. M. "Bell Number Diagrams." https://mathforum.org/advanced/robertd/bell.html.
Dickau, R. "Visualizing Combinatorial Enumeration." Mathematica in Educ. Res. 8, 11-18, 1999.
Gardner, M. "The Tinkly Temple Bells." Ch. 2 in Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 24-38, 1992.
Gould, H. W. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, 6th ed. Morgantown, WV: Math Monongliae, 1985.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Lenard, A. In Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. (M. Gardner). New York: W. H. Freeman, pp. 35-36, 1992.
Larrosa Canestro, I. "Bell(2841) Is Prime." Feb. 13, 2004. https://groups.yahoo.com/group/primenumbers/message/14558.
Levine, J. and Dalton, R. E. "Minimum Periods, Modulo  , of First Order Bell Exponential Integrals." Math. Comput. 16, 416-423, 1962.
, of First Order Bell Exponential Integrals." Math. Comput. 16, 416-423, 1962.
Lovász, L. Combinatorial Problems and Exercises, 2nd ed. Amsterdam, Netherlands: North-Holland, 1993.
Lunnon, W. F.; Pleasants, P. A. B.; and Stephens, N. M. "Arithmetic Properties of Bell Numbers to a Composite Modulus, I." Acta Arith. 35, 1-16, 1979.
Odlyzko, A. M. "Asymptotic Enumeration Methods." In Handbook of Combinatorics, Vol. 2 (Ed. R. L. Graham, M. Grötschel, and L. Lovász). Cambridge, MA: MIT Press, pp. 1063-1229, 1995. https://www.dtc.umn.edu/~odlyzko/doc/asymptotic.enum.pdf.
Penson, K. A.; Blasiak, P.; Duchamp, G.; Horzela, A.; and Solomon, A. I. "Hierarchical Dobiński-Type Relations via Substitution and the Moment Problem." 26 Dec 2003. https://www.arxiv.org/abs/quant-ph/0312202/.
Pitman, J. "Some Probabilistic Aspects of Set Partitions." Amer. Math. Monthly 104, 201-209, 1997.
Rota, G.-C. "The Number of Partitions of a Set." Amer. Math. Monthly 71, 498-504, 1964.
Sixdeniers, J.-M.; Penson, K. A.; and Solomon, A. I. "Extended Bell and Stirling Numbers from Hypergeometric Functions." J. Integer Sequences 4, No. 01.1.4, 2001. https://www.math.uwaterloo.ca/JIS/VOL4/SIXDENIERS/bell.html.
Sloane, N. J. A. Sequences A000110/M1484, A000178/M2049, A051130, A051131, A054767, and A113015 in "The On-Line Encyclopedia of Integer Sequences."
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, pp. 33-34, 1999.
Stanley, R. P. Enumerative Combinatorics, Vol. 2. Cambridge, England: Cambridge University Press, p. 13, 1999.
Wilson, D. "Bell Number Question." math-fun@cs.arizona.edu mailing list. 16 Jul 2007.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|