


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-9-2020
Date: 3-2-2021
Date: 2-11-2020
|
A prime number (or prime integer, often simply called a "prime" for short) is a positive integer  that has no positive integer divisors other than 1 and
that has no positive integer divisors other than 1 and  itself. More concisely, a prime number
itself. More concisely, a prime number  is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. For example, the only divisors of 13 are 1 and 13, making 13 a prime number, while the number 24 has divisors 1, 2, 3, 4, 6, 8, 12, and 24 (corresponding to the factorization
is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. For example, the only divisors of 13 are 1 and 13, making 13 a prime number, while the number 24 has divisors 1, 2, 3, 4, 6, 8, 12, and 24 (corresponding to the factorization  ), making 24 not a prime number. Positive integers other than 1 which are not prime are called composite numbers.
), making 24 not a prime number. Positive integers other than 1 which are not prime are called composite numbers.
While the term "prime number" commonly refers to prime positive integers, other types of primes are also defined, such as the Gaussian primes.
The number 1 is a special case which is considered neither prime nor composite (Wells 1986, p. 31). Although the number 1 used to be considered a prime (Goldbach 1742; Lehmer 1909, 1914; Hardy and Wright 1979, p. 11; Gardner 1984, pp. 86-87; Sloane and Plouffe 1995, p. 33; Hardy 1999, p. 46), it requires special treatment in so many definitions and applications involving primes greater than or equal to 2 that it is usually placed into a class of its own. A good reason not to call 1 a prime number is that if 1 were prime, then the statement of the fundamental theorem of arithmetic would have to be modified since "in exactly one way" would be false because any  . In other words, unique factorization into a product of primes would fail if the primes included 1. A slightly less illuminating but mathematically correct reason is noted by Tietze (1965, p. 2), who states "Why is the number 1 made an exception? This is a problem that schoolboys often argue about, but since it is a question of definition, it is not arguable." As more simply noted by Derbyshire (2004, p. 33), "2 pays its way [as a prime] on balance; 1 doesn't."
. In other words, unique factorization into a product of primes would fail if the primes included 1. A slightly less illuminating but mathematically correct reason is noted by Tietze (1965, p. 2), who states "Why is the number 1 made an exception? This is a problem that schoolboys often argue about, but since it is a question of definition, it is not arguable." As more simply noted by Derbyshire (2004, p. 33), "2 pays its way [as a prime] on balance; 1 doesn't."
With 1 excluded, the smallest prime is therefore 2. However, since 2 is the only even prime (which, ironically, in some sense makes it the "oddest" prime), it is also somewhat special, and the set of all primes excluding 2 is therefore called the "odd primes." Note also that while 2 is considered a prime today, at one time it was not (Tietze 1965, p. 18; Tropfke 1921, p. 96).
The  th prime number is commonly denoted
th prime number is commonly denoted  , so
, so  ,
,  , and so on, and may be computed in the Wolfram Language as Prime[n].
, and so on, and may be computed in the Wolfram Language as Prime[n].
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, ... (OEIS A000040; Hardy and Wright 1979, p. 3). A mnemonic for remembering the first seven primes is, "In the early morning, astronomers spiritualized nonmathematicians" (G. L. Honaker, Jr., pers. comm., Aug. 4, 2005). In the novel The Curious Incident of the Dog in the Night-Time (Haddon 2003), the protagonist Christopher amusingly numbers the chapters using the prime numbers instead of the (much) more traditional positive integers. In the Season 1 episode "Prime Suspect" (2005) of the television crime drama NUMB3RS, math genius Charlie Eppes realized that character Ethan's daughter has been kidnapped because he is close to solving the Riemann hypothesis, which allegedly would allow the perpetrators to break essentially all internet security by factoring large numbers.
The numbers of decimal digits in  for
for  , 1, ... is given by 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... (OEIS A099260).
, 1, ... is given by 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, ... (OEIS A099260).
The set of primes is sometimes denoted  , represented in the Wolfram Language as Primes.
, represented in the Wolfram Language as Primes.

The first few primes are illustrated above as a sequence of binary bits.
Euler commented "Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the mind will never penetrate" (Havil 2003, p. 163). In a 1975 lecture, D. Zagier commented "There are two facts about the distribution of prime numbers of which I hope to convince you so overwhelmingly that they will be permanently engraved in your hearts. The first is that, despite their simple definition and role as the building blocks of the natural numbers, the prime numbers grow like weeds among the natural numbers, seeming to obey no other law than that of chance, and nobody can predict where the next one will sprout. The second fact is even more astonishing, for it states just the opposite: that the prime numbers exhibit stunning regularity, that there are laws governing their behavior, and that they obey these laws with almost military precision" (Havil 2003, p. 171).
The  th prime for
th prime for  , 1, ... is given by 2, 29, 541, 7919, 104729, 1299709, 15485863, 179424673, 2038074743, ... (OEIS A006988; Graham et al. 1990, p. 111).
, 1, ... is given by 2, 29, 541, 7919, 104729, 1299709, 15485863, 179424673, 2038074743, ... (OEIS A006988; Graham et al. 1990, p. 111).
Large primes (Caldwell) include the large Mersenne primes, Ferrier's prime, and the  -digit counterexample
-digit counterexample  showing that 5359 is not a Sierpiński number of the second kind (Helm and Norris). The largest known prime as of December 2018 is the Mersenne prime
showing that 5359 is not a Sierpiński number of the second kind (Helm and Norris). The largest known prime as of December 2018 is the Mersenne prime  , which has a whopping
, which has a whopping  decimal digits.
decimal digits.
Prime numbers can be generated by sieving processes (such as the sieve of Eratosthenes), and lucky numbers, which are also generated by sieving, appear to share some interesting asymptotic properties with the primes. Prime numbers satisfy many strange and wonderful properties. Although there exist explicit prime formulas (i.e., formulas which either generate primes for all values or else the  th prime as a function of
th prime as a function of  ), they are contrived to such an extent that they are of little practical value.
), they are contrived to such an extent that they are of little practical value.
The Dirichlet generating function of the characteristic function of the prime numbers  is given by
is given by
![sum_(n=1)^(infty)([n in {p_k}_(k=1)^infty])/(n^s)](https://mathworld.wolfram.com/images/equations/PrimeNumber/Inline22.gif) |
 |
 |
(1) |
 |
 |
 |
(2) |
 |
 |
 |
(3) |
where  is the prime zeta function and
is the prime zeta function and ![[S]](https://mathworld.wolfram.com/images/equations/PrimeNumber/Inline32.gif) is an Iverson bracket.
is an Iverson bracket.
The function that gives the number of primes less than or equal to a number  is denoted
is denoted  and is called the prime counting function. The theorem giving an asymptotic form for
and is called the prime counting function. The theorem giving an asymptotic form for  is called the prime number theorem. Similarly, the numbers of primes of the form
is called the prime number theorem. Similarly, the numbers of primes of the form  less than or equal to a number
less than or equal to a number  is denoted
is denoted  and is called the modular prime counting function.
and is called the modular prime counting function.
 and
and  are inverse functions, so
are inverse functions, so
 |
(4) |
for all positive integers and
 |
(5) |
iff  is a prime number.
is a prime number.
Many prime factorization algorithms have been devised for determining the prime factors of a given integer, a process known as factorization or prime factorization. They vary quite a bit in sophistication and complexity. It is very difficult to build a general-purpose algorithm for this computationally "hard" problem, so any additional information which is known about the number in question or its factors can often be used to save a large amount of time. It should be emphasized that although no efficient algorithms are known for factoring arbitrary integers, it has not been proved that no such algorithm exists. It is therefore conceivable that a suitably clever person could devise a general method of factoring which would render the vast majority of encryption schemes in current widespread use, including those used by banks and governments, easily breakable.
Because of their importance in encryption algorithms such as RSA encryption, prime numbers can be important commercial commodities. In fact, R. Schlafly (1994) has obtained U.S. Patent  on the following two primes (expressed in hexadecimal notation):
on the following two primes (expressed in hexadecimal notation):
 |
(6) |
and
 |
(7) |
The fundamental theorem of arithmetic states that any positive integer can be represented in exactly one way as a product of primes. Euclid's second theorem demonstrated that there are an infinite number of primes. However, it is not known if there are an infinite number of primes of the form  (Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208), whether there are an infinite number of twin primes (the twin prime conjecture), or if a prime can always be found between
(Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208), whether there are an infinite number of twin primes (the twin prime conjecture), or if a prime can always be found between  and
and  (Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). The latter two of these are two of Landau's problems.
(Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398). The latter two of these are two of Landau's problems.
The simplest method of finding factors is so-called "direct search factorization" (a.k.a. trial division). In this method, all possible factors are systematically tested using trial division to see if they actually divide the given number. It is practical only for very small numbers. More general (and complicated) methods include the elliptic curve factorization method and number field sieve factorization method.
It has been proven that the set of prime numbers is a Diophantine set (Ribenboim 1991, pp. 106-107).
With the exception of 2 and 3, all primes are of the form  , i.e.,
, i.e.,  (Bungus 1599, p. 399, quoted in Peano 1908, p. 59; Wells 1986, p. 68). For
(Bungus 1599, p. 399, quoted in Peano 1908, p. 59; Wells 1986, p. 68). For  an integer
an integer  ,
,  is prime iff the congruence equation
is prime iff the congruence equation
 |
(8) |
holds for  , 1, ...,
, 1, ...,  (Deutsch 1996), where
(Deutsch 1996), where  is a binomial coefficient. In addition, an integer
is a binomial coefficient. In addition, an integer  is prime iff
is prime iff
 |
(9) |
The first few composite  for which
for which ![n|[phi(n)+sigma(n)]](https://mathworld.wolfram.com/images/equations/PrimeNumber/Inline56.gif) are
are  , 560, 588, 1400, 23760, ... (OEIS A011774; Guy 1997), with a total of 18 such numbers less than
, 560, 588, 1400, 23760, ... (OEIS A011774; Guy 1997), with a total of 18 such numbers less than  .
.
Chen (1979) showed that for  sufficiently large, there always exists a number with at least two prime factors between
sufficiently large, there always exists a number with at least two prime factors between 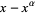 and
and  for
for 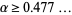 (Le Lionnais 1983, p. 26; Guy 2004, p. 34). In practice, this relation seems to hold for all
(Le Lionnais 1983, p. 26; Guy 2004, p. 34). In practice, this relation seems to hold for all 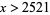 .
.
Primes consisting of consecutive digits (counting 0 as coming after 9) include 2, 3, 5, 7, 23, 67, 89, 4567, 78901, ... (OEIS A006510). Primes consisting of digits that are themselves primes include 23, 37, 53, 73, 223, 227, 233, 257, 277, 337, 353, 373, 523, 557, ... (OEIS A019546), which is one of the Smarandache sequences.
Because a prime number 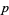 has only the trivial factors 1 and
has only the trivial factors 1 and 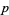 , in his The Road Ahead, Bill Gates accidentally referred to a trivial operation when he stated "Because both the system's privacy and the security of digital money depend on encryption, a breakthrough in mathematics or computer science that defeats the cryptographic system could be a disaster. The obvious mathematical breakthrough would be the development of an easy way to factor large prime numbers [emphasis added]" (Gates 1995, p. 265).
, in his The Road Ahead, Bill Gates accidentally referred to a trivial operation when he stated "Because both the system's privacy and the security of digital money depend on encryption, a breakthrough in mathematics or computer science that defeats the cryptographic system could be a disaster. The obvious mathematical breakthrough would be the development of an easy way to factor large prime numbers [emphasis added]" (Gates 1995, p. 265).
REFERENCES:
Berndt, B. C. "Ramanujan's Theory of Prime Numbers." Ch. 24 in Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Booker, A. "The Nth Prime Page." https://primes.utm.edu/nthprime/.
Bungus, P. Numerorum Mysteria. 1599.
Caldwell, C. "Largest Primes." https://www.utm.edu/research/primes/largest.html.
Caldwell, C. "The Largest Known Primes." https://primes.utm.edu/primes/lists/all.txt.
Caldwell, C. K. "The Top Twenty: Largest Known Primes." https://www.utm.edu/research/primes/lists/top20/Largest.html.
Chen, J. R. "On the Distribution of Almost Primes in an Interval II." Sci. Sinica 22, 253-275, 1979.
Cipra, B. A. "Math Team Vaults over Prime Record." Science 245, 815, 1989.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 130, 1996.
Courant, R. and Robbins, H. "The Prime Numbers." §1 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 21-31, 1996.
Crandall, R. and Pomerance, C. Prime Numbers. New York: Springer-Verlag, 2001.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Deutsch, E. "Problem 1494." Math. Mag. 69, 143, 1996.
Dickson, L. E. "Factor Tables, Lists of Primes." Ch. 13 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 347-356, 2005.
Ellison, W. J. and Ellison, F. Prime Numbers. New York: Wiley, 1985.
Eynden, C. V. "A Proof of Gandhi's Formula for the 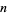 th Prime." Amer. Math. Monthly 79, 625, 1972.
th Prime." Amer. Math. Monthly 79, 625, 1972.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, 1984.
Gates, B. The Road Ahead. New York: Viking, 1995.
Giblin, P. J. Primes and Programming: Computers and Number Theory. New York: Cambridge University Press, 1994.
Glaisher, J. Factor Tables for the Sixth Million: Containing the Least Factor of Every Number Not Divisible by 2, 3, or 5 Between 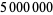 and
and 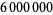 . London: Taylor and Francis, 1883.
. London: Taylor and Francis, 1883.
Goldbach, C. Letter to L. Euler, June 7, 1742. https://www.mathstat.dal.ca/~joerg/pic/g-letter.jpg or https://www.informatik.uni-giessen.de/staff/richstein/pic/g-letter-zoomed.jpg.
Golomb, S. W. "A Direct Interpretation of Gandhi's Formula." Amer. Math. Monthly 81, 752-754.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, 1990.
Guy, R. K. "Prime Numbers," "Formulas for Primes," and "Products Taken over Primes." Ch. A, §A17, and §B48 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 3-43, 36-41 and 102-103, 1994.
Guy, R. K. "Divisors and Desires." Amer. Math. Monthly 104, 359-360, 1997.
Guy, R. K. Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, 2004.
Haddon, M. The Curious Incident of the Dog in the Night-Time. New York: Vintage, 2003.
Hardy, G. H. Ch. 2 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "Prime Numbers" and "The Sequence of Primes." §1.2 and 1.4 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1-4, 11, 19, and 415, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem." https://www.seventeenorbust.com/.
Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem--Project Statistics." https://www.seventeenorbust.com/stats/.
Honaker, G. L. Jr. "Prime Curios!" https://primes.utm.edu/curios/.
Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., p. 30, 1976.
Kraitchik, M. "Prime Numbers." §3.9 in Mathematical Recreations. New York: W. W. Norton, pp. 78-79, 1942.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 26, 30, and 46, 1983.
Lehmer, D. N. Factor Table for the First Ten Millions, Containing the Smallest Factor of Every Number Not Divisible by 2, 3, 5 or 7 Between the Limits 0 and 10017000. Washington, DC: Carnegie Institution of Washington, No. 105, 1909.
Lehmer, D. N. List of Prime Numbers from 1 to 10006721. Washington, DC: Carnegie Institution, 1914.
Moser, L. "Notes on Number Theory III. On the Sum of Consecutive Primes." Can. Math. Bull. 6, 159-161, 1963.
Nagell, T. "Primes." §3 in Introduction to Number Theory. New York: Wiley, pp. 13-14, 1951.
Ore, Ø. Number Theory and Its History. New York: Dover, 1988.
Pappas, T. "Prime Numbers." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 100-101, 1989.
Peano, G. "Arithmetica." Ch. 2 in Formulario Mathematico. Torino, Italy, 1908.
Ramachandra, K. "Many Famous Conjectures on Primes; Meagre but Precious Progress of a Deep Nature." Proc. Indian Nat. Sci. Acad. Part A 64, 643-650, 1998.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, 1991.
Ribenboim, P. "Prime Number Records." Coll. Math. J. 25, 280-290, 1994.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, 1994.
Salamin, E. Item 53 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 22, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item53.
Schroeppel, R. Item 29 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 13, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item29.
Schlafly, R. "Partial Modular Reduction Method." United States Patent 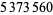 . December 13, 1994.
. December 13, 1994.
Sloane, N. J. A. Sequences A000040/M0652, A006510/M0679, A006988/M2151, A010051, A011774, A019546, A046024, and A099260 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
Tietze, H. "Prime Numbers and Prime Twins." Ch. 1 in Famous Problems of Mathematics: Solved and Unsolved Mathematics Problems from Antiquity to Modern Times. New York: Graylock Press, pp. 1-20, 1965.
Torelli, G. Sulla totalità dei numeri primi fino ad un limite assegnato. Naples, Italy: Tip. della Reale accad. della scienze fisiche e matematiche, 1901.
Tropfke, J. Geschichte der Elementar-Mathematik, Band 1. Berlin: p. 96, 1921.
Wagon, S. "Prime Numbers." Ch. 1 in Mathematica in Action. New York: W. H. Freeman, pp. 11-37, 1991.
Weisstein, E. W. "44th Mersenne Prime Found." MathWorld Headline News, Sep. 11, 2006. https://mathworld.wolfram.com/news/2006-09-11/mersenne-44/.
Weisstein, E. W. "Books about Prime Numbers." https://www.ericweisstein.com/encyclopedias/books/PrimeNumbers.html.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.
Zaiger, D. "The First 50 Million Prime Numbers." Math. Intel. 0, 221-224, 1977.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|