


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-8-2020
Date: 19-12-2019
Date: 24-12-2020
|
Mann's theorem is a theorem widely circulated as the "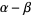 conjecture" that was subsequently proven by Mann (1942). It states that if
conjecture" that was subsequently proven by Mann (1942). It states that if 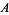 and
and 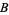 are sets of integers each containing 0, then
are sets of integers each containing 0, then
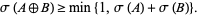 |
Here, 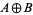 denotes the direct sum, i.e.,
denotes the direct sum, i.e., 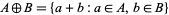 , and
, and 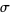 is the Schnirelmann density.
is the Schnirelmann density.
Mann's theorem is optimal in the sense that 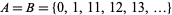 satisfies
satisfies 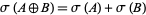 .
.
Mann's theorem implies Schnirelmann's theorem as follows. Let 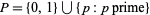 , then Mann's theorem proves that
, then Mann's theorem proves that 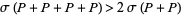 , so as more and more copies of the primes are included, the Schnirelmann density increases at least linearly, and so reaches 1 with at most
, so as more and more copies of the primes are included, the Schnirelmann density increases at least linearly, and so reaches 1 with at most 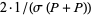 copies of the primes. Since the only sets with Schnirelmann density 1 are the sets containing all positive integers, Schnirelmann's theorem follows.
copies of the primes. Since the only sets with Schnirelmann density 1 are the sets containing all positive integers, Schnirelmann's theorem follows.
REFERENCES:
Garrison, B. K. "A Nontransformation Proof of Mann's Density Theorem." J. reine angew. Math. 245, 41-46, 1970.
Khinchin, A. Y. "The Landau-Schnirelmann Hypothesis and Mann's Theorem." Ch. 2 in Three Pearls of Number Theory. New York: Dover, pp. 18-36, 1998.
Mann, H. B. "A Proof of the Fundamental Theorem on the Density of Sets of Positive Integers." Ann. Math. 43, 523-527, 1942.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|