


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-1-2021
Date: 14-9-2020
Date: 2-11-2019
|
Landau's problems are the four "unattackable" problems mentioned by Landau in the 1912 Fifth Congress of Mathematicians in Cambridge, namely:
1. The Goldbach conjecture,
2. Twin prime conjecture,
3. Legendre's conjecture that for every 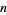 there exists a prime
there exists a prime 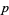 between
between 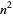 and
and 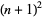 (Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398), and
(Hardy and Wright 1979, p. 415; Ribenboim 1996, pp. 397-398), and
4. The conjecture that there are infinitely many primes 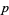 of the form
of the form 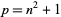 (Euler 1760; Mirsky 1949; Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208). The first few such primes are 2, 5, 17, 37, 101, 197, 257, 401, ... (OEIS A002496).
(Euler 1760; Mirsky 1949; Hardy and Wright 1979, p. 19; Ribenboim 1996, pp. 206-208). The first few such primes are 2, 5, 17, 37, 101, 197, 257, 401, ... (OEIS A002496).
Although it is not known if there always exists a prime 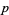 between
between 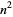 and
and 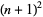 , Chen (1975) has shown that a number
, Chen (1975) has shown that a number 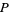 which is either a prime or semiprime does always satisfy this inequality. Moreover, there is always a prime between
which is either a prime or semiprime does always satisfy this inequality. Moreover, there is always a prime between 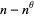 and
and 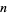 where
where 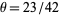 (Iwaniec and Pintz 1984; Hardy and Wright 1979, p. 415). The smallest primes between
(Iwaniec and Pintz 1984; Hardy and Wright 1979, p. 415). The smallest primes between 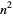 and
and 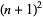 for
for 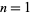 , 2, ..., are 2, 5, 11, 17, 29, 37, 53, 67, 83, ... (OEIS A007491).
, 2, ..., are 2, 5, 11, 17, 29, 37, 53, 67, 83, ... (OEIS A007491).
The first few primes 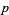 which are of the form
which are of the form 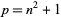 are given by 2, 5, 17, 37, 101, 197, 257, 401, ... (OEIS A002496). These correspond to
are given by 2, 5, 17, 37, 101, 197, 257, 401, ... (OEIS A002496). These correspond to 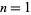 , 2, 4, 6, 10, 14, 16, 20, ... (OEIS A005574; Hardy and Wright 1979, p. 19).
, 2, 4, 6, 10, 14, 16, 20, ... (OEIS A005574; Hardy and Wright 1979, p. 19).
REFERENCES:
Chen, J. R. "On the Distribution of Almost Primes in an Interval." Sci. Sinica 18, 611-627, 1975.
Euler, L. "De numeris primis valde magnis." Novi Commentarii academiae scientiarum Petropolitanae 9, 99-153, (1760) 1764. Reprinted in Commentat. arithm. 1, 356-378, 1849. Reprinted in Opera Omnia: Series 1, Volume 3, pp. 1-45.
Goldman, J. R. The Queen of Mathematics: An Historically Motivated Guide to Number Theory. Wellesley, MA: A K Peters, p. 22, 1998.
Hardy, G. H. and Wright, W. M. "Unsolved Problems Concerning Primes." §2.8 and Appendix §3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 19 and 415-416, 1979.
Iwaniec, H. and Pintz, J. "Primes in Short Intervals." Monatsh. f. Math. 98, 115-143, 1984.
Ogilvy, C. S. Tomorrow's Math: Unsolved Problems for the Amateur, 2nd ed. Oxford, England: Oxford University Press, p. 116, 1972.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 132-134 and 206-208, 1996.
Sloane, N. J. A. Sequences A002496/M1506, A005574/M1010, and A007491/M1389 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
العتبة الحسينية تطلق فعاليات المخيم القرآني الثالث في جامعة البصرة
|
|
|