


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-11-2019
Date: 4-1-2021
Date: 14-4-2020
|
A recursive primality certificate for a prime 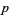 . The certificate consists of a list of
. The certificate consists of a list of
1. A point on an elliptic curve 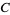
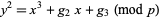 |
for some numbers 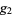 and
and 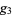 .
.
2. A prime 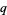 with
with 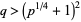 , such that for some other number
, such that for some other number 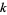 and
and 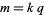 with
with 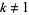 ,
, 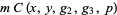 is the identity on the curve, but
is the identity on the curve, but 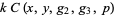 is not the identity. This guarantees primality of
is not the identity. This guarantees primality of 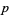 by a theorem of Goldwasser and Kilian (1986).
by a theorem of Goldwasser and Kilian (1986).
3. Each 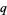 has its recursive certificate following it. So if the smallest
has its recursive certificate following it. So if the smallest 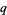 is known to be prime, all the numbers are certified prime up the chain.
is known to be prime, all the numbers are certified prime up the chain.
A Pratt certificate is quicker to generate for small numbers. The Wolfram Language task ProvablePrimeQ[n] in the Wolfram Language package PrimalityProving` therefore generates an Atkin-Goldwasser-Kilian-Morain certificate only for numbers above a certain limit (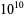 by default), and a Pratt certificate for smaller numbers.
by default), and a Pratt certificate for smaller numbers.
REFERENCES:
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Bressoud, D. M. Factorization and Primality Testing. New York: Springer-Verlag, 1989.
Goldwasser, S. and Kilian, J. "Almost All Primes Can Be Quickly Certified." Proc. 18th STOC. pp. 316-329, 1986.
Morain, F. "Implementation of the Atkin-Goldwasser-Kilian Primality Testing Algorithm." Rapport de Recherche 911, INRIA, Octobre 1988.
Schoof, R. "Elliptic Curves over Finite Fields and the Computation of Square Roots mod 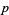 ." Math. Comput. 44, 483-494, 1985.
." Math. Comput. 44, 483-494, 1985.
Wunderlich, M. C. "A Performance Analysis of a Simple Prime-Testing Algorithm." Math. Comput. 40, 709-714, 1983.a



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق دراسة تناقش تجربة المركز العراقي لتوثيق جرائم التطرف وتعاونه مع كراسي اليونسكو في الجامعات العراقية
|
|
|