


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-6-2020
Date: 22-2-2020
Date: 8-1-2020
|
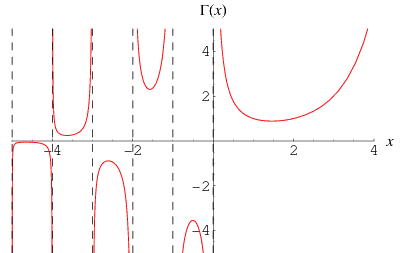
The (complete) gamma function 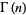 is defined to be an extension of the factorial to complex and real number arguments. It is related to the factorial by
is defined to be an extension of the factorial to complex and real number arguments. It is related to the factorial by
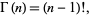 |
(1) |
a slightly unfortunate notation due to Legendre which is now universally used instead of Gauss's simpler 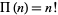 (Gauss 1812; Edwards 2001, p. 8).
(Gauss 1812; Edwards 2001, p. 8).
It is analytic everywhere except at 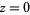 ,
, 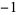 ,
, 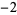 , ..., and the residue at
, ..., and the residue at 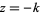 is
is
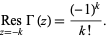 |
(2) |
There are no points 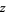 at which
at which 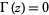 .
.
The gamma function is implemented in the Wolfram Language as Gamma[z].
There are a number of notational conventions in common use for indication of a power of a gamma functions. While authors such as Watson (1939) use 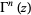 (i.e., using a trigonometric function-like convention), it is also common to write
(i.e., using a trigonometric function-like convention), it is also common to write ![[Gamma(z)]^n](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline10.gif) .
.
The gamma function can be defined as a definite integral for ![R[z]>0](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline11.gif) (Euler's integral form)
(Euler's integral form)
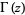 |
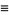 |
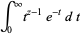 |
(3) |
 |
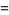 |
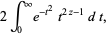 |
(4) |
or
![Gamma(z)=int_0^1[ln(1/t)]^(z-1)dt.](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation3.gif) |
(5) |
The complete gamma function  can be generalized to the upper incomplete gamma function
can be generalized to the upper incomplete gamma function 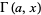 and lower incomplete gamma function
and lower incomplete gamma function 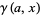 .
.
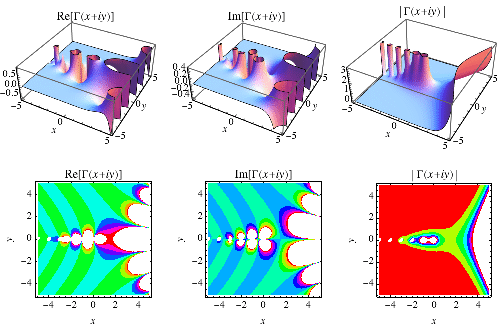 |
Plots of the real and imaginary parts of 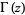 in the complex plane are illustrated above.
in the complex plane are illustrated above.
Integrating equation (3) by parts for a real argument, it can be seen that
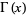 |
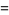 |
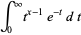 |
(6) |
 |
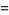 |
![[-t^(x-1)e^(-t)]_0^infty+int_0^infty(x-1)t^(x-2)e^(-t)dt](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline27.gif) |
(7) |
 |
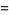 |
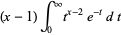 |
(8) |
 |
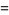 |
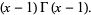 |
(9) |
If  is an integer
is an integer  , 2, 3, ..., then
, 2, 3, ..., then
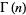 |
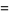 |
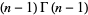 |
(10) |
 |
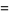 |
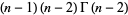 |
(11) |
 |
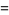 |
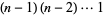 |
(12) |
 |
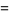 |
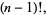 |
(13) |
so the gamma function reduces to the factorial for a positive integer argument.
A beautiful relationship between 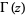 and the Riemann zeta function
and the Riemann zeta function 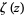 is given by
is given by
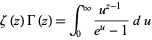 |
(14) |
for ![R[z]>1](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline50.gif) (Havil 2003, p. 60).
(Havil 2003, p. 60).
The gamma function can also be defined by an infinite product form (Weierstrass form)
![Gamma(z)=[ze^(gammaz)product_(r=1)^infty(1+z/r)e^(-z/r)]^(-1),](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation5.gif) |
(15) |
where 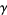 is the Euler-Mascheroni constant (Krantz 1999, p. 157; Havil 2003, p. 57). Taking the logarithm of both sides of (◇),
is the Euler-Mascheroni constant (Krantz 1999, p. 157; Havil 2003, p. 57). Taking the logarithm of both sides of (◇),
![-ln[Gamma(z)]=lnz+gammaz+sum_(n=1)^infty[ln(1+z/n)-z/n].](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation6.gif) |
(16) |
Differentiating,
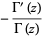 |
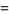 |
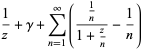 |
(17) |
 |
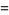 |
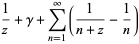 |
(18) |
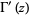 |
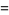 |
![-Gamma(z)[1/z+gamma+sum_(n=1)^(infty)(1/(n+z)-1/n)]](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline60.gif) |
(19) |
 |
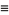 |
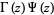 |
(20) |
 |
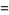 |
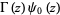 |
(21) |
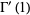 |
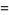 |
![-Gamma(1){1+gamma+[(1/2-1)+(1/3-1/2)+...+(1/(n+1)-1/n)+...]}](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline69.gif) |
(22) |
 |
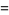 |
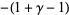 |
(23) |
 |
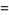 |
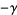 |
(24) |
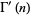 |
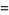 |
![-Gamma(n){1/n+gamma+[(1/(1+n)-1)+(1/(2+n)-1/2)+(1/(3+n)-1/3)+...]}](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline78.gif) |
(25) |
 |
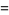 |
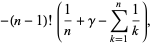 |
(26) |
where 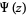 is the digamma function and
is the digamma function and 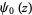 is the polygamma function.
is the polygamma function. 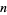 th derivatives are given in terms of the polygamma functions
th derivatives are given in terms of the polygamma functions 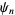 ,
, 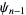 , ...,
, ..., 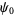 .
.
The minimum value  of
of  for real positive
for real positive  is achieved when
is achieved when
 |
(27) |
 |
(28) |
This can be solved numerically to give  (OEIS A030169; Wrench 1968), which has continued fraction [1, 2, 6, 63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (OEIS A030170). At
(OEIS A030169; Wrench 1968), which has continued fraction [1, 2, 6, 63, 135, 1, 1, 1, 1, 4, 1, 38, ...] (OEIS A030170). At  ,
,  achieves the value 0.8856031944... (OEIS A030171), which has continued fraction [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (OEIS A030172).
achieves the value 0.8856031944... (OEIS A030171), which has continued fraction [0, 1, 7, 1, 2, 1, 6, 1, 1, ...] (OEIS A030172).
The Euler limit form is
![Gamma(z)=1/zproduct_(n=1)^infty[(1+1/n)^z(1+z/n)^(-1)],](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation9.gif) |
(29) |
so
 |
 |
 |
(30) |
 |
 |
 |
(31) |
 |
 |
 |
(32) |
 |
 |
 |
(33) |
(Krantz 1999, p. 156).
One over the gamma function  is an entire function and can be expressed as
is an entire function and can be expressed as
![1/(Gamma(z))=zexp[gammaz-sum_(k=2)^infty((-1)^kzeta(k)z^k)/k],](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation10.gif) |
(34) |
where  is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and  is the Riemann zeta function (Wrench 1968). An asymptotic series for
is the Riemann zeta function (Wrench 1968). An asymptotic series for  is given by
is given by
![1/(Gamma(z))∼z+gammaz^2+1/(12)(6gamma^2-pi^2)z^3+1/(12)[2gamma^3-gammapi^2+4zeta(3)]z^4+....](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation11.gif) |
(35) |
Writing
 |
(36) |
the  satisfy
satisfy
 |
(37) |
(Bourguet 1883, Davis 1933, Isaacson and Salzer 1943, Wrench 1968). Wrench (1968) numerically computed the coefficients for the series expansion about 0 of
![1/(z(1+z)Gamma(z))=1+(gamma-1)z+[1+1/2(gamma-2)gamma-1/(12)pi^2]z^2+....](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation14.gif) |
(38) |
The Lanczos approximation gives a series expansion for  for
for  in terms of an arbitrary constant
in terms of an arbitrary constant  such that
such that ![R[z+sigma+1/2]>0](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline114.gif) .
.
The gamma function satisfies the functional equations
 |
 |
 |
(39) |
 |
 |
 |
(40) |
Additional identities are
 |
 |
 |
(41) |
 |
 |
 |
(42) |
 |
 |
 |
(43) |
 |
 |
 |
(44) |
Using (41), the gamma function  of a rational number
of a rational number  can be reduced to a constant times
can be reduced to a constant times  or
or  . For example,
. For example,
 |
 |
 |
(45) |
 |
 |
 |
(46) |
 |
 |
 |
(47) |
 |
 |
 |
(48) |
For ![R[z]=-1/2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline149.gif) ,
,
 |
(49) |
Gamma functions of argument  can be expressed using the Legendre duplication formula
can be expressed using the Legendre duplication formula
 |
(50) |
Gamma functions of argument  can be expressed using a triplication formula
can be expressed using a triplication formula
 |
(51) |
The general result is the Gauss multiplication formula
 |
(52) |
The gamma function is also related to the Riemann zeta function  by
by
 |
(53) |
For integer  , 2, ..., the first few values of
, 2, ..., the first few values of  are 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, ... (OEIS A000142). For half-integer arguments,
are 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, ... (OEIS A000142). For half-integer arguments,  has the special form
has the special form
 |
(54) |
where  is a double factorial. The first few values for
is a double factorial. The first few values for  , 3, 5, ... are therefore
, 3, 5, ... are therefore
 |
 |
 |
(55) |
 |
 |
 |
(56) |
 |
 |
 |
(57) |
 ,
,  , ... (OEIS A001147 and A000079; Wells 1986, p. 40). In general, for
, ... (OEIS A001147 and A000079; Wells 1986, p. 40). In general, for  a positive integer
a positive integer  , 2, ...
, 2, ...
 |
 |
 |
(58) |
 |
 |
 |
(59) |
 |
 |
 |
(60) |
 |
 |
 |
(61) |
Simple closed-form expressions of this type do not appear to exist for  for
for  a positive integer
a positive integer  . However, Borwein and Zucker (1992) give a variety of identities relating gamma functions to square roots and elliptic integral singular values
. However, Borwein and Zucker (1992) give a variety of identities relating gamma functions to square roots and elliptic integral singular values  , i.e., elliptic moduli
, i.e., elliptic moduli  such that
such that
 |
(62) |
where  is a complete elliptic integral of the first kind and
is a complete elliptic integral of the first kind and  is the complementary integral. M. Trott (pers. comm.) has developed an algorithm for automatically generating hundreds of such identities.
is the complementary integral. M. Trott (pers. comm.) has developed an algorithm for automatically generating hundreds of such identities.
 |
 |
![2^(7/9)3^(-1/12)pi^(1/3)[K(k_3)]^(1/3)](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline192.gif) |
(63) |
 |
 |
![2pi^(1/4)[K(k_1)]^(1/2)](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline195.gif) |
(64) |
 |
 |
![2^(-1/3)3^(1/2)pi^(-1/2)[Gamma(1/3)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline198.gif) |
(65) |
 |
 |
 |
(66) |
 |
 |
![2(sqrt(2)+1)^(1/2)pi^(-1/4)[K(k_1)]^(1/2)](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline204.gif) |
(67) |
 |
 |
 |
(68) |
 |
 |
 |
(69) |
 |
 |
 |
(70) |
 |
 |
 |
(71) |
 |
 |
![2^(25/18)3^(1/3)(sqrt(2)+1)pi^(-1/3)[K(k_3)]^(2/3)](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline219.gif) |
(72) |
 |
 |
![384(sqrt(2)+1)(sqrt(3)-sqrt(2))(2-sqrt(3))pi[K(k_6)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline222.gif) |
(73) |
 |
 |
 |
(74) |
 |
 |
 |
(75) |
 |
 |
![2·3^(1/2)5^(1/6)sin(2/(15)pi)[Gamma(1/3)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline231.gif) |
(76) |
 |
 |
![2^2·3^(2/5)sin(1/5pi)sin(4/(15)pi)[Gamma(1/5)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline234.gif) |
(77) |
 |
 |
![(2^(-3/2)3^(-1/5)5^(1/4)(sqrt(5)-1)^(1/2)[Gamma(2/5)]^2)/(sin(4/(15)pi))](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline237.gif) |
(78) |
 |
 |
![60(sqrt(5)-1)sin(7/(15)pi)[K(k_(15))]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline240.gif) |
(79) |
 |
 |
 |
(80) |
 |
 |
![2^(4/5)(10-2sqrt(5))^(1/2)pi^(-1)sin(7/(20)pi)sin(9/(20)pi)[Gamma(1/5)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline246.gif) |
(81) |
 |
 |
![2^(3/5)(10+2sqrt(5))^(1/2)pi^(-1)sin(3/(20)pi)sin(9/(20)pi)[Gamma(2/5)]^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline249.gif) |
(82) |
 |
 |
![160(sqrt(5)-2)^(1/2)pi[K(k_5)]^2.](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline252.gif) |
(83) |
Several of these are also given in Campbell (1966, p. 31).
A few curious identities include
 |
 |
 |
(84) |
 |
 |
 |
(85) |
 |
 |
 |
(86) |
 |
 |
 |
(87) |
 |
 |
 |
(88) |
 |
 |
 |
(89) |
 |
 |
 |
(90) |
of which Magnus and Oberhettinger (1949, p. 1) give only the last case and
 |
(91) |
(Magnus and Oberhettinger 1949, p. 1). Ramanujan also gave a number of fascinating identities:
![(Gamma^2(n+1))/(Gamma(n+xi+1)Gamma(n-xi+1))=product_(k=1)^infty[1+(x^2)/((n+k)^2)]](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation23.gif) |
(92) |
 |
(93) |
where
![phi(m,n)=product_(k=1)^infty[1+((m+n)/(k+m))^3],](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation25.gif) |
(94) |
![product_(k=1)^infty[1+(n/k)^3]product_(k=1)^infty[1+3(n/(n+2k))^2]=(Gamma(1/2n))/(Gamma[1/2(n+1)])(cosh(pinsqrt(3))-cos(pin))/(2^(n+2)pi^(3/2)n)](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation26.gif) |
(95) |
(Berndt 1994).
Ramanujan gave the infinite sums
![sum_(k=0)^infty(8k+1)[(Gamma(k+1/4))/(k!Gamma(1/4))]^4
=1+9(1/4)^4+17((1·5)/(4·8))^4+25((1·5·9)/(4·8·12))^4+...
=(2^(3/2))/(sqrt(pi)[Gamma(3/4)]^2)](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation27.gif) |
(96) |
and
![sum_(k=0)^infty(-1)^k(4k+1)[((2k-1)!!)/((2k)!!)]^5
=1-5(1/2)^5+9((1·3)/(2·4))^5-13((1·3·5)/(2·4·6))^5+...
=2/([Gamma(3/4)]^4)](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation28.gif) |
(97) |
(Hardy 1923; Hardy 1924; Whipple 1926; Watson 1931; Bailey 1935; Hardy 1999, p. 7).
The following asymptotic series is occasionally useful in probability theory (e.g., the one-dimensional random walk):
 |
(98) |
(OEIS A143503 and A061549; Graham et al. 1994). This series also gives a nice asymptotic generalization of Stirling numbers of the first kind to fractional values.
It has long been known that  is transcendental (Davis 1959), as is
is transcendental (Davis 1959), as is  (Le Lionnais 1983; Borwein and Bailey 2003, p. 138), and Chudnovsky has apparently recently proved that
(Le Lionnais 1983; Borwein and Bailey 2003, p. 138), and Chudnovsky has apparently recently proved that  is itself transcendental (Borwein and Bailey 2003, p. 138).
is itself transcendental (Borwein and Bailey 2003, p. 138).
There exist efficient iterative algorithms for  for all integers
for all integers  (Borwein and Bailey 2003, p. 137). For example, a quadratically converging iteration for
(Borwein and Bailey 2003, p. 137). For example, a quadratically converging iteration for  (OEIS A068466) is given by defining
(OEIS A068466) is given by defining
 |
 |
 |
(99) |
 |
 |
 |
(100) |
setting  and
and  , and then
, and then
![Gamma(1/4)=2(1+sqrt(2))^(3/4)[product_(n=1)^inftyx_n^(-1)((1+x_n)/(1+y_n))^3]^(1/4)](https://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation30.gif) |
(101) |
(Borwein and Bailey 2003, pp. 137-138).
No such iteration is known for  (Borwein and Borwein 1987; Borwein and Zucker 1992; Borwein and Bailey 2003, p. 138).
(Borwein and Borwein 1987; Borwein and Zucker 1992; Borwein and Bailey 2003, p. 138).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Gamma (Factorial) Function" and "Incomplete Gamma Function." §6.1 and 6.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 255-258 and 260-263, 1972.
Arfken, G. "The Gamma Function (Factorial Function)." Ch. 10 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 339-341 and 539-572, 1985.
Artin, E. The Gamma Function. New York: Holt, Rinehart, and Winston, 1964.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 334-342, 1994.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 218, 1987.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 6, 1987.
Borwein, J. M. and Zucker, I. J. "Fast Evaluation of the Gamma Function for Small Rational Fractions Using Complete Elliptic Integrals of the First Kind." IMA J. Numerical Analysis 12, 519-526, 1992.
Bourguet, L. "Sur les intégrales Eulériennes et quelques autres fonctions uniformes." Acta Math. 2, 261-295, 1883.
Campbell, R. Les intégrales eulériennes et leurs applications. Paris: Dunod, 1966.
Davis, H. T. Tables of the Higher Mathematical Functions. Bloomington, IN: Principia Press, 1933.
Davis, P. J. "Leonhard Euler's Integral: A Historical Profile of the Gamma Function." Amer. Math. Monthly 66, 849-869, 1959.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Gamma Function." Ch. 1 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 1-55, 1981.
Finch, S. R. "Euler-Mascheroni Constant." §1.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 28-40, 2003.
Gauss, C. F. "Disquisitiones Generales Circa Seriem Infinitam ![[(alphabeta)/(1·gamma)]x+[(alpha(alpha+1)beta(beta+1))/(1·2·gamma(gamma+1))]x^2](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline289.gif)
![+[(alpha(alpha+1)(alpha+2)beta(beta+1)(beta+2))/(1·2·3·gamma(gamma+1)(gamma+2))]x^3+](https://mathworld.wolfram.com/images/equations/GammaFunction/Inline290.gif) etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.
etc. Pars Prior." Commentationes Societiones Regiae Scientiarum Gottingensis Recentiores, Vol. II. 1812. Reprinted in Gesammelte Werke, Bd. 3, pp. 123-163 and 207-229, 1866.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to Problem 9.60 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc. (Records of Proceedings at Meetings) 22, xii-xiii, 1924.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. "The Gamma Function." Ch. 6 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 53-60, 2003.
Isaacson, E. and Salzer, H. E. "Mathematical Tables--Errata: 19. J. P. L. Bourget, 'Sur les intégrales Eulériennes et quelques autres fonctions uniformes,' Acta Mathematica, v. 2, 1883, pp. 261-295.' " Math. Tab. Aids Comput. 1, 124, 1943.
Koepf, W. "The Gamma Function." Ch. 1 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 4-10, 1998.
Krantz, S. G. "The Gamma and Beta Functions." §13.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 155-158, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Magnus, W. and Oberhettinger, F. Formulas and Theorems for the Special Functions of Mathematical Physics. New York: Chelsea, 1949.
Nielsen, N. "Handbuch der Theorie der Gammafunktion." Part I in Die Gammafunktion. New York: Chelsea, 1965.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Gamma Function, Beta Function, Factorials, Binomial Coefficients" and "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.1 and 6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 206-209 and 209-214, 1992.
Sloane, N. J. A. Sequences A000079/M1129, A000142/M1675, A001147/M3002, A030169, A030170, A030171, A030172, A061549, A068466, and A143503 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Gamma Function  " and "The Incomplete Gamma
" and "The Incomplete Gamma  and Related Functions." Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
and Related Functions." Chs. 43 and 45 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 411-421 and 435-443, 1987.
Watson, G. N. "Theorems Stated by Ramanujan (XI)." J. London Math. Soc. 6, 59-65, 1931.
Watson, G. N. "Three Triple Integrals." Quart. J. Math., Oxford Ser. 2 10, 266-276, 1939.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 40, 1986.
Whipple, F. J. W. "A Fundamental Relation between Generalised Hypergeometric Series." J. London Math. Soc. 1, 138-145, 1926.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Wrench, J. W. Jr. "Concerning Two Series for the Gamma Function." Math. Comput. 22, 617-626, 1968.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|