Kloosterman's Sum

Kloosterman's sum is defined by

(1)

where 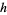 runs through a complete set of residues relatively prime to  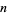and 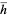 is defined by

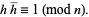(2)

The notation 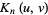 is also used, at least for prime .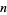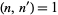

If  (if 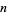 and 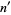 are relatively prime), then

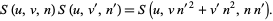(3)

Kloosterman's sum essentially solves the problem introduced by Ramanujan of representing sufficiently large numbers by quadratic forms 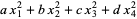. Weil improved on Kloosterman's estimate for Ramanujan's problem with the best possible estimate

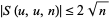(4)

(Duke 1997).

REFERENCES:

Duke, W. "Some Old Problems and New Results about Quadratic Forms." Not. Amer. Math. Soc. 44, 190-196, 1997.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 56, 1979.

Katz, N. M. Gauss Sums, Kloosterman Sums, and Monodromy Groups. Princeton, NJ: Princeton University Press, 1987.

Kloosterman, H. D. "On the Representation of Numbers in the Form 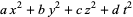." Acta Math. 49, 407-464, 1926.

Kloosterman, H. D. "The Behavior of General Theta Functions under the Modular Group and the Characters of Binary Modular Congruence Groups, I." Ann. Math. 47, 317-375, 1946.

Kloosterman, H. D. "The Behavior of General Theta Functions under the Modular Group and the Characters of Binary Modular Congruence Groups, II." Ann. Math. 47, 376-447, 1946.

Malyšev, A. V. "Gauss and Kloosterman Sums." Dokl. Akad. Nauk SSSR 133, 1017-1020, 1960. English translation in Soviet Math. Dokl. 1, 928-932, 1960.

Ramanujan, S. "On the Expression of a Number in the Form 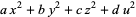." In Collected Papers of Srinivasa Ramanujan. (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., 2000.