


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-1-2021
Date: 11-3-2020
Date: 5-1-2020
|
The odd divisor function
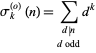 |
(1) |
is the sum of 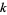 th powers of the odd divisors of a number
th powers of the odd divisors of a number 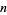 . It is the analog of the divisor function for odd divisors only.
. It is the analog of the divisor function for odd divisors only.
For the case 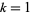 ,
,
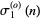 |
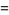 |
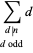 |
(2) |
 |
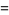 |
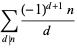 |
(3) |
 |
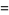 |
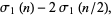 |
(4) |
where 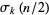 is defined to be 0 if
is defined to be 0 if 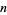 is odd. The generating function is given by
is odd. The generating function is given by
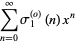 |
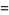 |
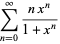 |
(5) |
 |
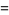 |
![1/(24)[theta_3^4(x)+theta_2^4(x)]](https://mathworld.wolfram.com/images/equations/OddDivisorFunction/Inline20.gif) |
(6) |
 |
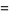 |
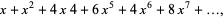 |
(7) |
where 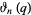 is a Jacobi elliptic function.
is a Jacobi elliptic function.
Rather surprisingly, 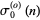 gives the number of factors of the polynomial
gives the number of factors of the polynomial 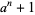 .
.
The following table gives the first few 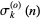 .
.
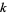 |
OEIS | 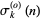 |
| 0 | A001227 | 1, 1, 2, 1, 2, 2, 2, 1, 3, 2, ... |
| 1 | A000593 | 1, 1, 4, 1, 6, 4, 8, 1, 13, 6, ... |
| 2 | A050999 | 1, 1, 10, 1, 26, 10, 50, 1, 91, 26, ... |
| 3 | A051000 | 1, 1, 28, 1, 126, 28, 344, 1, 757, 126, ... |
| 4 | A051001 | 1, 1, 82, 1, 626, 82, 2402, 1, 6643, 626, ... |
| 5 | A051002 | 1, 1, 244, 1, 3126, 244, 16808, 1, 59293, 3126, ... |
This function arises in Ramanujan's Eisenstein series 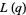 and in a recurrence relation for the partition function P.
and in a recurrence relation for the partition function P.
REFERENCES:
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 306, 2005.
Hirzebruch, F. Manifolds and Modular Forms, 2nd ed. Braunschweig, Germany: Vieweg, p. 133, 1994.
Riordan, J. Combinatorial Identities. New York: Wiley, p. 187, 1979.
Sloane, N. J. A. Sequences A000593/M3197, A001227, A050999, A051000, A051001, and A051002 in "The On-Line Encyclopedia of Integer Sequences."
Verhoeff, T. "Rectangular and Trapezoidal Arrangements." J. Integer Sequences 2, #99.1.6, 1999.a



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|