Dirichlet Divisor Problem

Let the divisor function 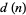 be the number of divisors of  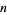(including  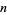itself). For a prime 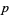, 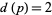. In general,

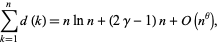where 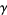 is the Euler-Mascheroni constant. Dirichlet originally gave  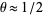(Hardy and Wright 1979, p. 264; Hardy 1999, pp. 67-68), and Hardy and Landau showed in 1916 that  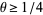(Hardy 1999, p. 81). The following table summarizes incremental progress on the upper limit (updating Hardy 1999, p. 81).

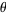	approx.	citation
1/2	0.50000	Dirichlet
1/3	0.33333	Voronoi (1903), Sierpiński (1906), van der Corput (1923)
37/112	0.33036	Littlewood and Walfisz (1925)
33/100	0.33000	van der Corput (1922)
27/82	0.32927	van der Corput (1928)
15/46	0.32609
12/37	0.32432	Chen (1963), Kolesnik (1969)
35/108	0.32407	Kolesnik (1982)
139/429	0.32401	Kolesnik
17/53	0.32075	Vinogradov (1935)
7/22	0.31818	Iwaniec and Mozzochi (1988)
23/73	0.31507	Huxley (1993)
131/416	0.31490	Huxley (2003)

REFERENCES:

Bohr, H. and Cramér, H. "Ellipsoidprobleme." In "Die neuere Entwicklung der analytischen Zahlentheorie." Ch. IIC88 in Enzykl. d. Math. Wiss., Vol. 2, Part 3, Issue 2 II C 8, 823-824, 1922.

Chen, J.-R. "The Lattice-Points in a Circle." Sci. Sinica 12, 633-649, 1963.

Graham, S. W. and Kolesnik, G. Van Der Corput's Method of Exponential Sums. Cambridge, England: Cambridge University Press, 1991.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Huxley, M. N. "Exponential Sums and Lattice Points." Proc. London Math. Soc. 60, 471-502, 1990.

Huxley, M. N. "Corrigenda: 'Exponential Sums and Lattice Points.' " Proc. London Math. Soc. 66, 70, 1993.

Huxley, M. N. "Exponential Sums and Lattice Points. II." Proc. London Math. Soc. 66, 279-301, 1993.

Huxley, M. N. "Exponential Sums and Lattice Points III." Proc. London Math. Soc. 87, 5910-609, 2003.

Iwaniec, H. and Mozzochi, C. J. "On the Divisor and Circle Problem." J. Numb. Th. 29, 60-93, 1988.

Kolesnik, G. A. "An Improvement of the Remainder Term in the Divisor Problem." Mat. Zametki 6, 545-554, 1969. English translation in Math. Notes 6, 784-791, 1969.

Kolesnik, G. "On the Order of 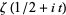 and 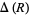." Pacific J. Math. 98, 107-122, 1982.

Littlewood, J. E. and Walfisz, A. "The Lattice Points of a Circle. (With a Note by Prof. E. Landau.)." Proc. Roy. Soc. London (A) 106, 478-488, 1925.

van der Corput, J. G. "Zum Teilerproblem." Math. Ann. 98, 697-716, 1928.