


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2021
Date: 20-10-2020
Date: 8-3-2020
|
The number 10 (ten) is the basis for the decimal system of notation. In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the 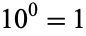 s place. For example, the number 1234.56 specifies
s place. For example, the number 1234.56 specifies
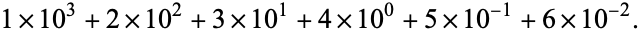 |
(1) |
The decimal places to the left of the decimal point are 1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, ... (OEIS A011557), called one, ten, hundred, thousand, ten thousand, hundred thousand, million, 10 million, 100 million, and so on. The names of subsequent decimal places for large numbers differ depending on country. Any power of 10 which can be written as the product of two numbers not containing 0s must be of the form 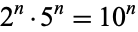 for
for 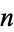 an integer such that neither
an integer such that neither 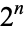 nor
nor 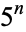 contains any zeros. The largest known such number is
contains any zeros. The largest known such number is
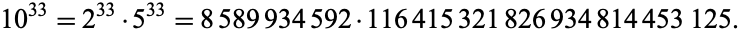 |
(2) |
A complete list of such known numbers is
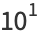 |
 |
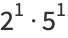 |
(3) |
 |
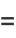 |
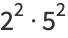 |
(4) |
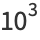 |
 |
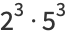 |
(5) |
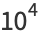 |
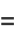 |
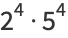 |
(6) |
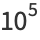 |
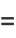 |
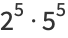 |
(7) |
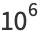 |
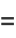 |
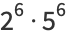 |
(8) |
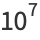 |
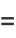 |
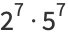 |
(9) |
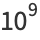 |
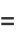 |
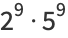 |
(10) |
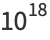 |
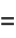 |
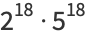 |
(11) |
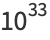 |
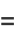 |
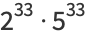 |
(12) |
(Madachy 1979). Since all powers of 2 with exponents 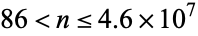 contain at least one zero (M. Cook, pers. comm., Sept. 26, 1997), no other power of ten less than 46 million can be written as the product of two numbers not containing 0s.
contain at least one zero (M. Cook, pers. comm., Sept. 26, 1997), no other power of ten less than 46 million can be written as the product of two numbers not containing 0s.
REFERENCES:
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 127-128, 1979.
Pickover, C. A. Keys to Infinity. New York: Wiley, p. 135, 1995.
Sloane, N. J. A. Sequence A011557 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 76-82, 1986.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
وفد كلية الزراعة في جامعة كربلاء يشيد بمشروع الحزام الأخضر
|
|
|