Brjuno Number

Let 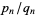 be the sequence of convergents of the continued fraction of a number 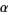. Then a Brjuno number is an irrational number such that

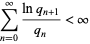(Marmi et al. 1997, 2001). Brjuno numbers arise in the study of one-dimensional analytic small divisors problems, and Brjuno (1971, 1972) proved that all "germs" with linear part 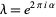 are linearizable if  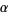is a Brjuno number. Yoccoz (1995) proved that this condition is also necessary.

REFERENCES:

Brjuno, A. D. "Analytical Form of Differential Equations." Trans. Moscow Math. Soc. 25, 131-288, 1971.

Brjuno, A. D. "Analytical Form of Differential Equations. II." Trans. Moscow Math. Soc. 26, 199-239, 1972.

Marmi, S.; Moussa, P.; and Yoccoz, J.-C. "The Brjuno Functions and Their Regularity Properties." Comm. Math. Phys. 186, 265-293, 1997.

Marmi, S.; Moussa, P.; and Yoccoz, J.-C. "Complex Brjuno Functions." J. Amer. Math. Soc. 14, 783-841, 2001.

Siegel, C. L. "Iteration of Analytic Functions." Ann. Math. 43, 807-812, 1942.

Yoccoz, J.-C. "Théorème de Siegel, nombres de Bruno et polynômes quadratiques." Astérique 231, 3-88, 1995.