Linear Congruence Equation

A linear congruence equation

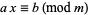(1)

is solvable iff the congruence

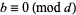(2)

with 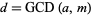 is the greatest common divisor is solvable. Let one solution to the original equation be 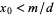. Then the solutions are 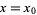, , 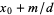, 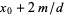..., 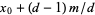. If 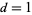, then there is only one solution .

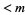The solution of a linear congruence can be found in the Wolfram Language using Reduce[a*x == b, x, Modulus -> m].

Solution to a linear congruence equation is equivalent to finding the value of a fractional congruence, for which a greedy-type algorithm exists. In particular, (1) can be rewritten as

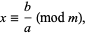(3)

which can also be written

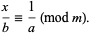(4)

In this form, the solution  can be found as Mod[b y, m] of the solution 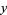 returned by the Wolfram Language function PowerMod[a, 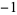, m]. This is known as a modular inverse.

Two or more simultaneous linear congruences

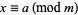(5)

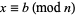(6)

are solvable using the Chinese remainder theorem.

REFERENCES:

Nagell, T. "Linear Congruences." §23 in Introduction to Number Theory. New York: Wiley, pp. 76-78, 1951.