Prime Products
المؤلف:
Grosswald, E
المصدر:
"Some Number Theoretical Products." Rev. Columbiana Mat. 21
الجزء والصفحة:
...
11-10-2020
2223
Prime Products
The product of primes
 |
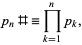(1)
|
with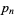 
the 
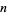th prime, is called the primorial function, by analogy with the factorial function. Its logarithm is closely related to the Chebyshev function 
.
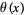The zeta-regularized product over all primes is given by
(Muñoz Garcia and Pérez-Marco 2003, 2008), answering the question posed by Soulé et al. (1992, p. 101). A derivation proceeds by algebraic manipulation of the prime zeta function and gives the more general results
 |
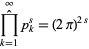(4)
|
and
 |
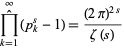(5)
|
(Muñoz Garcia and Pérez-Marco 2003).
Mertens theorem states that
 |
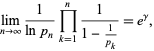(6)
|
where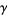 
is the Euler-Mascheroni constant, and a closely related result is given by
 |
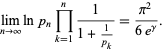(7)
|
There are amazing infinite product formulas for primes given by
 |
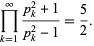(8)
|
(Ramanujan 1913-1914; Le Lionnais 1983, p. 46) and
 |
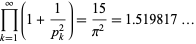(9)
|
(OEIS A082020; Ramanujan 1913-1914).
More general formulas are given by
 |
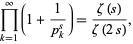(10)
|
where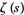 
is the Riemann zeta function and by the Euler product
 |
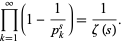(11)
|
Named prime products include Barban's constant
(OEIS A175640), the Feller-Tornier constant
(OEIS A065493), Heath-Brown-Moroz constant
(OEIS A118228), Murata's constant
(OEIS A065485), the quadratic class number constant
(OEIS A065465), Sarnak's constant
(OEIS A065476), and Taniguchi's constant
(OEIS A175639), where the product is over the primes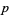 
.
Define the number theoretic character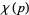 
by
![chi(p)=<span style=]() {+1 if p=1 (mod 4); -1 if p=3 (mod 4), " src="https://mathworld.wolfram.com/images/equations/PrimeProducts/NumberedEquation10.gif" style="height:41px; width:183px" /> |
(26)
|
then
(OEIS A060294; Oakes 2003). Similarly,
(Oakes 2004). This is equivalent to the formula due to Euler
(Blatner 1997).
Let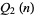 
be the number of consecutive numbers 
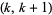with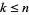 
such that 
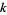and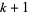 
are both squarefree. Then 
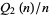is given asymptotically by
 |
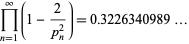(37)
|
(OEIS A065474), where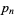 
is the 
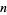th prime.
REFERENCES:
Blatner, D. The Joy of Pi. New York: Walker, p. 110, 1997.
Grosswald, E. "Some Number Theoretical Products." Rev. Columbiana Mat. 21, 231-242, 1987.
Guy, R. K. "Products Taken over Primes." §B87 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 102-103, 1994.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is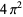 
." Preprint IHES/M/03/34. May 2003. https://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is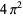 
." Commun. Math. Phys. 277, 69-81, 2008.
Niklasch, G. "Some Number-Theoretical Constants Arising as Products of Rational Functions of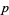 
over the Primes." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Oakes, M. "Re: [PrimeNumbers] pi=(2/1) (3/2) (5/6) (7/6) (11/10) (13/14) (17/18) (19/18)...." Dec. 21, 2003. https://groups.yahoo.com/group/primenumbers/message/14257.
Oakes, M. "Re: primes and pi." Jan. 29, 2004. https://groups.yahoo.com/group/primenumbers/message/14486.
Ramanujan, S. "Modular Equations and Approximations to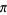 
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Sloane, N. J. A. Sequences A065465, A065474, A065485, A065493, A082020, A118228, A175639, and A175640 in "The On-Line Encyclopedia of Integer Sequences."
Soulé, C.; Abramovich, D.; Burnois, J. F.; and Kramer, J. Lectures on Arakelov Geometry. Cambridge, England: Cambridge University Press, 1992.
Uchiyama, S. "On Some Products Involving Primes." Proc. Amer. Math. Soc. 28, 629-630, 1971.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
