


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-1-2021
Date: 26-5-2020
Date: 9-1-2020
|
A base-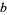 BBP-type formula is a convergent series formula of the type
BBP-type formula is a convergent series formula of the type
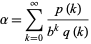 |
(1) |
where 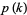 and
and 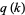 are integer polynomials in
are integer polynomials in 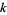 (Bailey 2000; Borwein and Bailey 2003, pp. 54 and 128-129).
(Bailey 2000; Borwein and Bailey 2003, pp. 54 and 128-129).
Bailey (2000) and Borwein and Bailey (2003, pp. 128-129) give a collection of such formulas. The following extends those compilations to include several additional BBP-type formulas.
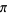 |
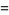 |
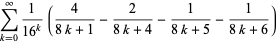 |
(2) |
 |
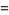 |
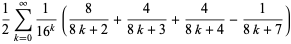 |
(3) |
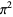 |
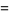 |
![9/8sum_(k=0)^(infty)1/(64^k)[(16)/((6k+1)^2)-(24)/((6k+2)^2)-8/((6k+3)^2)-6/((6k+4)^2)+1/((6k+5)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline13.gif) |
(4) |
 |
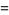 |
![2/(27)sum_(k=0)^(infty)1/(729^k)[(243)/((12k+1)^2)-(405)/((12k+2)^2)-(81)/((12k+4)^4)-(27)/((12k+5)^2)-(72)/((12k+6)^2)-9/((12k+7)^2)-9/((12k+8)^2)-5/((12k+10)^2)+1/((12k+11)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline16.gif) |
(5) |
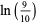 |
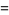 |
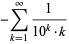 |
(6) |
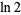 |
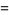 |
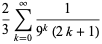 |
(7) |
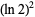 |
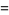 |
![1/(32)sum_(k=0)^(infty)[(64)/((6k+1)^2)-(160)/((6k+2)^2)-(56)/((6k+3)^2)-(40)/((6k+4)^2)+4/((6k+5)^2)-1/((6k+6)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline25.gif) |
(8) |
 |
 |
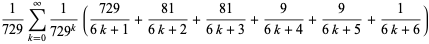 |
(9) |
 |
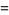 |
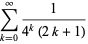 |
(10) |
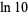 |
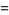 |
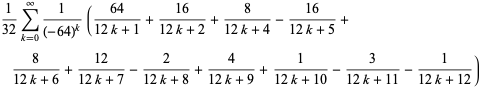 |
(11) |
 |
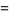 |
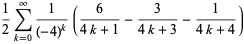 |
(12) |
 |
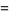 |
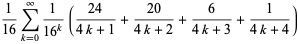 |
(13) |
 |
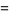 |
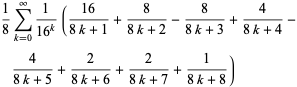 |
(14) |
 |
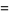 |
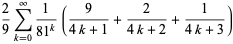 |
(15) |
 |
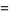 |
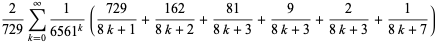 |
(16) |
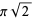 |
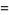 |
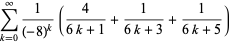 |
(17) |
 |
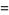 |
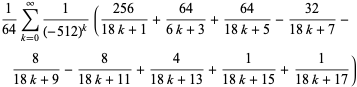 |
(18) |
 |
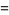 |
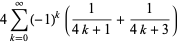 |
(19) |
 |
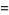 |
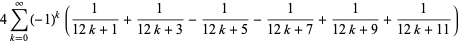 |
(20) |
 |
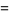 |
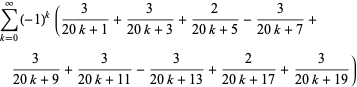 |
(21) |
 |
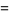 |
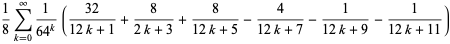 |
(22) |
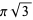 |
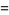 |
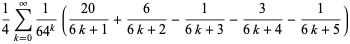 |
(23) |
 |
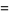 |
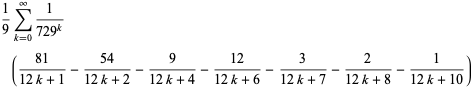 |
(24) |
 |
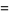 |
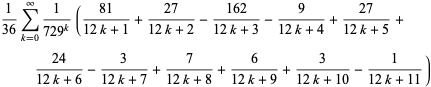 |
(25) |
 |
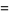 |
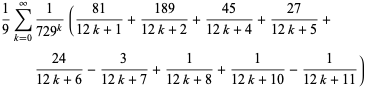 |
(26) |
 |
 |
![1/(256)sum_(k=0)^(infty)1/(4096^k)[(4096)/((24k+1)^2)-(8192)/((24k+2)^2)-(26112)/((24k+3)^3)+(15360)/((24k+4)^2)-(1024)/((24k+5)^2)+(9984)/((24k+6)^2)+(11520)/((24k+8)^2)+(2368)/((24k+9)^2)-(512)/((24k+10)^2)+(768)/((24k+12)^2)-(64)/((24k+13)^2)+(408)/((24k+15)^2)+(720)/((24k+16)^2)+(16)/((24k+17)^2)+(196)/((24k+18)^2)+(60)/((24k+20)^2)-(37)/((24k+21)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline82.gif) |
(27) |
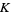 |
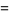 |
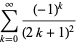 |
(28) |
 |
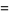 |
![1/(1024)sum_(k=0)^(infty)1/(4096^k)[(3072)/((24k+1)^2)-(3072)/((24k+2)^2)-(23040)/((24k+3)^2)+(12288)/((24k+4)^2)-(768)/((24k+5)^2)+(9216)/((24k+6)^2)+(10368)/((24k+8)^2)+(2496)/((24k+9)^2)-(192)/((24k+10)^2)+(768)/((24k+12)^2)-(48)/((24k+13)^2)+(360)/((24k+15)^2)+(648)/((24k+16)^2)+(12)/((24k+17)^2)+(168)/((24k+18)^2)+(48)/((24k+20)^2)-(39)/((24k+21)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline88.gif) |
(29) |
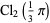 |
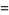 |
![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+1/((6k+2)^2)-1/((6k+4)^2)-1/((6k+5)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline91.gif) |
(30) |
 |
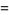 |
![(sqrt(3))/9sum_(k=0)^(infty)((-1)^k)/(27^k)[(18)/((6k+1)^2)-(18)/((6k+2)^2)-(24)/((6k+3)^2)-6/((6k+4)^2)+2/((6k+5)^2)].](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/Inline94.gif) |
(31) |
where 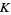 is Catalan's constant,
is Catalan's constant, 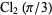 is the hyperbolic volume of the figure eight knot complement,
is the hyperbolic volume of the figure eight knot complement, 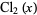 is Clausen's integral, and
is Clausen's integral, and 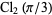 is also the hyperbolic volume of the knot complement of the figure eight knot.
is also the hyperbolic volume of the knot complement of the figure eight knot.
Another example is the Dirichlet L-series
![L_(-7)(2)=sum_(n=0)^infty[1/((7n+1)^2)+1/((7n+2)^2)-1/((7n+3)^2)+1/((7n+4)^2)-1/((7n+5)^2)-1/((7n+6)^2)]](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/NumberedEquation2.gif) |
(32) |
(Bailey and Borwein 2005; Bailey et al. 2007, pp. 5 and 62).
Note that this sort of sum is closely related to the polygamma function since, for example, the above sum can also be written
![L_(-7)(2)=1/(49)[psi_1(1/7)+psi_1(2/7)-psi_1(3/7)+psi_1(4/7)-psi_1(5/7)-psi_1(6/7)].](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/NumberedEquation3.gif) |
(33) |
Borwein et al. (2004) have recently shown that 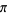 has no Machin-type BBP arctangent formula that is not binary, although this does not rule out a completely different scheme for digit-extraction algorithms in other bases.
has no Machin-type BBP arctangent formula that is not binary, although this does not rule out a completely different scheme for digit-extraction algorithms in other bases.
A beautiful example of a BBP-type formula in a non-integer base is
![pi^2=50sum_(k=0)^infty1/(phi^(5k))[(phi^(-2))/((5k+1)^2)-(phi^(-1))/((5k+2)^2)-(phi^(-2))/((5k+3)^2)+(phi^(-5))/((5k+4)^2)+(2phi^(-5))/((5k+5)^2)],](https://mathworld.wolfram.com/images/equations/BBP-TypeFormula/NumberedEquation4.gif) |
(34) |
where 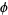 is the golden ratio, found by B. Cloitre (Cloitre; Borwein and Chamberland 2005; Bailey et al. 2007, p. 277).
is the golden ratio, found by B. Cloitre (Cloitre; Borwein and Chamberland 2005; Bailey et al. 2007, p. 277).
REFERENCES:
Adamchik, V. and Wagon, S. "A Simple Formula for 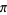 ." Amer. Math. Monthly 104, 852-855, 1997.
." Amer. Math. Monthly 104, 852-855, 1997.
Adamchik, V. and Wagon, S. "Pi: A 2000-Year Search Changes Direction." http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
Bailey, D. H. "A Compendium of BBP-Type Formulas for Mathematical Constants." 28 Nov 2000. http://crd.lbl.gov/~dhbailey/dhbpapers/bbp-formulas.pdf.
Bailey, D. H. and Borwein, J. M. "Experimental Mathematics: Examples, Methods, and Implications." Not. Amer. Math. Soc. 52, 502-514, 2005.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 31-33 and 222, 2007.
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Borwein, J. and Bailey, D. "Other BBP-Type Formulas" and "Does Pi Have a Nonbinary BBP Formula?" §3.6 and 3.7 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 127-133, 2003.
Borwein, J. M.; Borwein, D.; and Galway, W. F. "Finding and Excluding 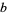 -ary Machin-Type Individual Digit Formulae." Canad. J. Math. 56, 897-925, 2004.
-ary Machin-Type Individual Digit Formulae." Canad. J. Math. 56, 897-925, 2004.
Borwein, J. M. and Chamberland, M. "A Golden Example." Unpublished manuscript. Feb. 7, 2005.
Cloitre, B. "A BBP Formula for 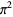 in Golden Base." Unpublished manuscript. Undated.
in Golden Base." Unpublished manuscript. Undated.
Finch, S. R. "Archimedes' Constant." §1.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 17-28, 2003.
Gourévitch, B. "L'univers de 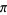 . §6: Formules BBP en base 2:
. §6: Formules BBP en base 2: 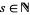 ,
, 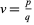 ,
, 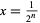 dans
dans 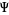 ." http://www.pi314.net/hypergse6.php.
." http://www.pi314.net/hypergse6.php.
Plouffe, S. "The Story Behind a Formula for Pi." sci.math and sci.math.symbolic newsgroup posting. 23 Jun 2003.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق مدير كرسي اليونسكو في جامعة الموصل يقدّم دراسةً تناقش استراتيجية الكرسي لنبذ التطرف وتعزيز ثقافة السلام
|
|
|