

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Cunningham Number
المؤلف:
Mudge, M.
المصدر:
"Not Numerology but Numeralogy!" Personal Computer World
الجزء والصفحة:
...
1-1-2021
1247
Cunningham Number
A Cunningham number is a binomial number of the form 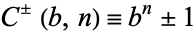 with
with 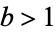 and
and 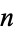 positive integers. Bases
positive integers. Bases 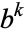 which are themselves powers need not be considered since they correspond to
which are themselves powers need not be considered since they correspond to 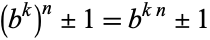 . Prime numbers of the form
. Prime numbers of the form 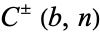 are very rare.
are very rare.
A necessary (but not sufficient) condition for 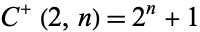 to be prime is that
to be prime is that 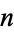 be of the form
be of the form 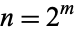 . Numbers of the form
. Numbers of the form 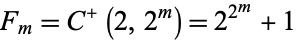 are called Fermat numbers, and the only known primes occur for
are called Fermat numbers, and the only known primes occur for 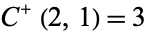 ,
, 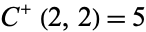 ,
, 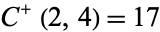 ,
, 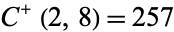 , and
, and 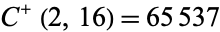 (i.e.,
(i.e., 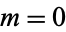 , 1, 2, 3, 4). The only other primes
, 1, 2, 3, 4). The only other primes 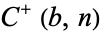 for nontrivial
for nontrivial 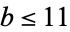 and
and 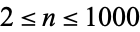 are
are 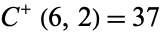 ,
, 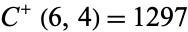 , and
, and 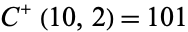 .
.
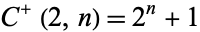 is always divisible by 3 when
is always divisible by 3 when 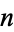 is odd.
is odd.
Primes of the form 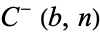 are also very rare. The Mersenne numbers
are also very rare. The Mersenne numbers 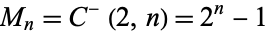 are known to be prime only for 44 values, the first few of which are
are known to be prime only for 44 values, the first few of which are 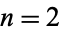 , 3, 5, 7, 13, 17, 19, ... (OEIS A000043). Such numbers are known as Mersenne primes. There are no other primes
, 3, 5, 7, 13, 17, 19, ... (OEIS A000043). Such numbers are known as Mersenne primes. There are no other primes 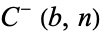 for nontrivial
for nontrivial 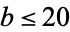 and
and 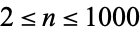 .
.
In 1925, Cunningham and Woodall (1925) gathered together all that was known about the primality and factorization of the numbers 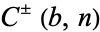 and published a small book of tables. These tables collected from scattered sources the known prime factors for the bases 2 and 10 and also presented the authors' results of 30 years' work with these and other bases.
and published a small book of tables. These tables collected from scattered sources the known prime factors for the bases 2 and 10 and also presented the authors' results of 30 years' work with these and other bases.
Since 1925, many people have worked on filling in these tables. D. H. Lehmer, a well-known mathematician who died in 1991, was for many years a leader of these efforts. Lehmer was a mathematician who was at the forefront of computing as modern electronic computers became a reality. He was also known as the inventor of some ingenious pre-electronic computing devices specifically designed for factoring numbers.
Updated factorizations were published in Brillhart et al. (1988). The tables have been extended by Brent and te Riele (1992) to 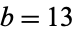 , ..., 100 with
, ..., 100 with 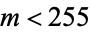 for
for 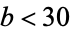 and
and 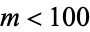 for
for 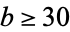 . All numbers with exponent 58 and smaller, and all composites with
. All numbers with exponent 58 and smaller, and all composites with 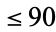 digits have now been factored.
digits have now been factored.
REFERENCES:
Brent, R. P. and te Riele, H. J. J. "Factorizations of 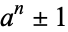 ,
, 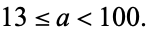 " Report NM-R9212, Centrum voor Wiskunde en Informatica. Amsterdam, June 1992. https://web.comlab.ox.ac.uk/oucl/work/richard.brent/pub/pub200.html.
" Report NM-R9212, Centrum voor Wiskunde en Informatica. Amsterdam, June 1992. https://web.comlab.ox.ac.uk/oucl/work/richard.brent/pub/pub200.html.
Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Tuckerman, B.; and Wagstaff, S. S. Jr. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, 3rd ed. Providence, RI: Amer. Math. Soc., 1988. https://www.ams.org/online_bks/conm22/.
Cunningham, A. J. C. and Woodall, H. J. Factorisation of y-n∓1, y=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers (n). London: Hodgson, 1925.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Ribenboim, P. "Numbers 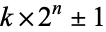 ." §5.7 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 355-360, 1996.
." §5.7 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 355-360, 1996.
Sloane, N. J. A. Sequence A000043/M0672 in "The On-Line Encyclopedia of Integer Sequences."
Wagstaff, S. S. Jr. "The Cunningham Project." https://www.cerias.purdue.edu/homes/ssw/cun/.
Wagstaff, S. S. Jr. "The Third Edition of the Cunningham Books." https://www.cerias.purdue.edu/homes/ssw/cun/third/.a
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















