المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Robbins Constant |
 636
 05:40 مساءً
date: 12-2-2020 |
Author : Finch, S. R. 
Book or Source : "Geometric Probability Constants." §8.1 in Mathematical Constants. Cambridge, England: Cambridge University Press 
Page and Part : ...|
Read More
Date: 18-5-2020
550
Date: 22-8-2020
525
Date: 27-10-2019
669
|
The Robbins constant is the mean line segment length, i.e., the expected distance between two points chosen at random in cube line picking, namely
 |
 |
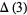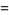![1/(105)[4+17sqrt(2)-6sqrt(3)+21ln(1+sqrt(2))+42ln(2+sqrt(3))-7pi]](http://mathworld.wolfram.com/images/equations/RobbinsConstant/Inline3.gif) |
(1) |
 |
 |
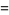![1/(105)[4+17sqrt(2)-6sqrt(3)+21sinh^(-1)1+42ln(2+sqrt(3))-7pi]](http://mathworld.wolfram.com/images/equations/RobbinsConstant/Inline6.gif) |
(2) |
 |
 |
 |
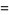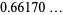(3) |
(OEIS A073012; Robbins 1978, Le Lionnais 1983).
REFERENCES:
Finch, S. R. "Geometric Probability Constants." §8.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 479-484, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 30, 1983.
Robbins, D. "Average Distance between Two Points in a Box." Amer. Math. Monthly 85, 278, 1978.
Sloane, N. J. A. Sequences A073012, A160693, and A160694 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
