


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2020
Date: 12-12-2020
Date: 2-2-2016
|

Pick three points 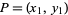 ,
, 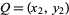 , and
, and 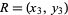 distributed independently and uniformly in a unit disk
distributed independently and uniformly in a unit disk 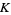 (i.e., in the interior of the unit circle). Then the average area of the triangle determined by these points is
(i.e., in the interior of the unit circle). Then the average area of the triangle determined by these points is
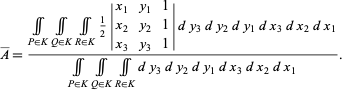 |
(1) |
Using disk point picking, this can be written as
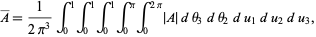 |
(2) |
where
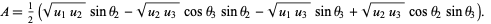 |
(3) |
A trigonometric substitution can then be used to remove the trigonometric functions and split the integral into
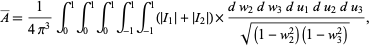 |
(4) |
where
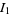 |
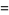 |
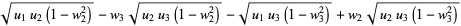 |
(5) |
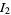 |
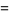 |
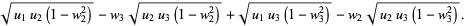 |
(6) |
However, the easiest way to evaluate the integral is using Crofton's formula and polar coordinates to yield a mean triangle area
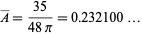 |
(7) |
for unit-radius disks (OEIS A189511), or
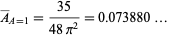 |
(8) |
for unit-area disks (OEIS A093587; Woolhouse 1867; Solomon 1978; Pfiefer 1989; Zinani 2003). This problem is very closely related to Sylvester's four-point problem, and can be derived as the limit as 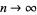 of the general polygon triangle picking problem.
of the general polygon triangle picking problem.
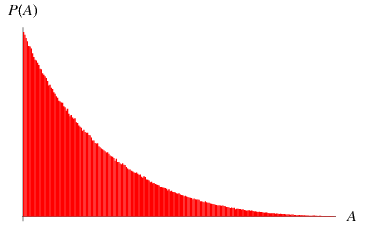
The distribution of areas, illustrated above, is apparently not known exactly.
The probability 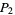 that three random points in a disk form an acute triangle is
that three random points in a disk form an acute triangle is
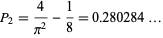 |
(9) |
(OEIS A093588; Woolhouse 1886). The problem was generalized by Hall (1982) to 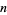 -dimensional ball triangle picking, and Buchta (1986) gave closed form evaluations for Hall's integrals.
-dimensional ball triangle picking, and Buchta (1986) gave closed form evaluations for Hall's integrals.
REFERENCES:
Buchta, C. "Zufallspolygone in konvexen Vielecken." J. reine angew. Math. 347, 212-220, 1984.
Buchta, C. "A Note on the Volume of a Random Polytope in a Tetrahedron." Ill. J. Math. 30, 653-659, 1986.
Guy, R. K. "There are Three Times as Many Obtuse-Angled Triangles as There are Acute-Angled Ones." Math. Mag. 66, 175-178, 1993.
Hall, G. R. "Acute Triangles in the 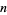 -Ball." J. Appl. Prob. 19, 712-715, 1982.
-Ball." J. Appl. Prob. 19, 712-715, 1982.
Pfiefer, R. E. "The Historical Development of J. J. Sylvester's Four Point Problem." Math. Mag. 62, 309-317, 1989.
Sloane, N. J. A. Sequences A093587, A093588, and A189511 in "The On-Line Encyclopedia of Integer Sequences."
Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, 1978.
Woolhouse, W. S. B. "Solution to Problem 1350." Mathematical Questions, with Their Solutions, from the Educational Times, Vol. 1. London: F. Hodgson and Son, pp. 22-23, Jul. 1863-Jun. 1864.
Woolhouse, W. S. B. "Some Additional Observations on the Four-Point Problem." Mathematical Questions, with Their Solutions, from the Educational Times, Vol. 7. London: F. Hodgson and Son, p. 81, 1867.
Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|