Cube Tetrahedron Picking

Given four points chosen at random inside a unit cube, the average volume of the tetrahedron determined by these points is given by

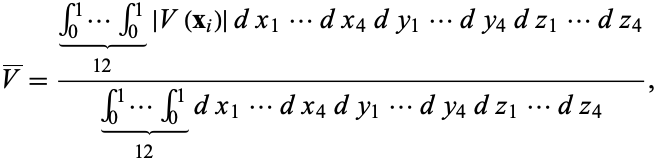(1)

where the polyhedron vertices are located at 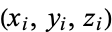 where 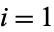, ..., 4, and the (signed) volume is given by the determinant

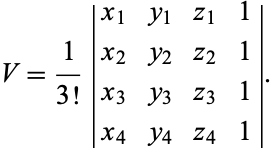(2)

The integral is extremely difficult to compute, but the analytic result for the mean tetrahedron volume is

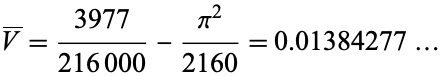(3)

(OEIS A093524; Zinani 2003). Note that the result quoted in the reply to Seidov (2000) actually refers to the average volume for tetrahedron tetrahedron picking.

REFERENCES:

Do, K.-A. and Solomon, H. "A Simulation Study of Sylvester's Problem in Three Dimensions." J. Appl. Prob. 23, 509-513, 1986.

Seidov, Z. F. "Letters: Random Triangle." Mathematica J. 7, 414, 2000.

Sloane, N. J. A. Sequence A093524 in "The On-Line Encyclopedia of Integer Sequences."

Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.