


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-1-2021
Date: 28-1-2021
Date: 7-12-2020
|
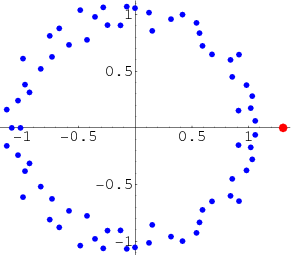
The constant
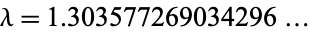 |
(OEIS A014715) giving the asymptotic rate of growth 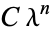 of the number of digits in the
of the number of digits in the 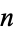 th term of the look and say sequence, given by the unique positive real root of the polynomial
th term of the look and say sequence, given by the unique positive real root of the polynomial
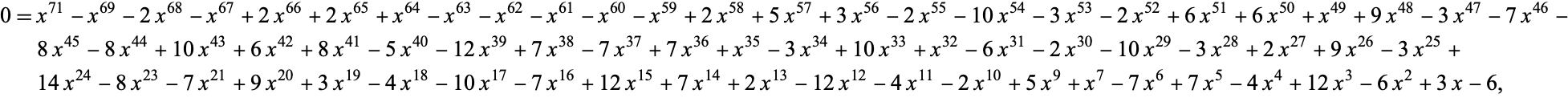 |
illustrated in the figure above. Note that the polynomial given in Conway (1987, p. 188) contains a misprint.
The continued fraction for 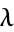 is 1, 3, 3, 2, 1, 2, 1, 5, 8, 4, 14, 3, 1, ... (OEIS A014967).
is 1, 3, 3, 2, 1, 2, 1, 5, 8, 4, 14, 3, 1, ... (OEIS A014967).
REFERENCES:
Conway, J. H. "The Weird and Wonderful Chemistry of Audioactive Decay." §5.11 in Open Problems in Communications and Computation (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 173-188, 1987.
Conway, J. H. and Guy, R. K. "The Look and Say Sequence." In The Book of Numbers. New York: Springer-Verlag, pp. 208-209, 1996.
Finch, S. R. "Conway's Constant." §6.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 452-455, 2003.
Hilgemeier, M. "Die Gleichniszahlen-Reihe." Bild der Wissensch. 12, 194-196, Dec. 1986.
Hilgemeier, M. "'One Metaphor Fits All': A Fractal Voyage with Conway's Audioactive Decay." Ch. 7 in Fractal Horizons: The Future Use of Fractals (Ed. C. A. Pickover). New York: St. Martin's Press, 1996.
Sloane, N. J. A. Sequences A014715 and A014967 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 13-14, 1991.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 905, 2002.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|