


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-2-2020
Date: 13-11-2019
Date: 24-10-2020
|
There are at least two statements which go by the name of Artin's conjecture.
If 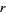 is any complex finite-dimensional representation of the absolute Galois group of a number field, then Artin showed how to associate an
is any complex finite-dimensional representation of the absolute Galois group of a number field, then Artin showed how to associate an 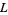 -series
-series 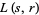 with it. These
with it. These 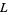 -series directly generalize zeta functions and Dirichlet
-series directly generalize zeta functions and Dirichlet 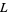 -series, and as a result of work by Richard Brauer,
-series, and as a result of work by Richard Brauer, 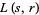 is known to extend to a meromorphic function on the complex plane. Artin's conjecture predicts that it is in fact holomorphic, i.e., has no poles, with the possible exception of a pole at
is known to extend to a meromorphic function on the complex plane. Artin's conjecture predicts that it is in fact holomorphic, i.e., has no poles, with the possible exception of a pole at 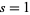 (Artin 1923/1924). Compare with the generalized Riemann hypothesis, which deals with the locations of the zeros of certain
(Artin 1923/1924). Compare with the generalized Riemann hypothesis, which deals with the locations of the zeros of certain 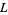 -series.
-series.
The second conjecture states that every integer not equal to 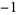 or a square number is a primitive root modulo
or a square number is a primitive root modulo 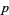 for infinitely many
for infinitely many 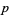 and proposes a density for the set of such
and proposes a density for the set of such 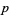 which are always rational multiples of a constant known as Artin's constant. There is an analogous theorem for functions instead of numbers which has been proved by Billharz (Shanks 1993, p. 147).
which are always rational multiples of a constant known as Artin's constant. There is an analogous theorem for functions instead of numbers which has been proved by Billharz (Shanks 1993, p. 147).
REFERENCES:
Artin, E. "Über eine neue Art von 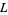 -Reihen." Abh. Math. Sem. Univ. Hamburg 3, 89-108, 1923/1924.
-Reihen." Abh. Math. Sem. Univ. Hamburg 3, 89-108, 1923/1924.
Matthews, K. R. "A Generalization of Artin's Conjecture for Primitive Roots." Acta Arith. 29, 113-146, 1976.
Moree, P. "A Note on Artin's Conjecture." Simon Stevin 67, 255-257, 1993.
Ram Murty, M. "Artin's Conjecture for Primitive Roots." Math. Intell. 10, 59-67, 1988.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 31, 80-83, and 147, 1993.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|