Lattice Method

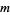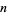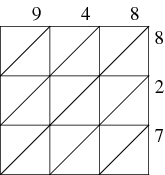
The lattice method is an alternative to long multiplication for numbers. In this approach, a lattice is first constructed, sized to fit the numbers being multiplied. If we are multiplying an -digit number by an -digit number, the size of the lattice is 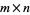. The multiplicand is placed along the top of the lattice so that each digit is the header for one column of cells (the most significant digit is put at the left). The multiplier is placed along the right side of the lattice so that each digit is a (trailing) header for one row of cells (the most significant digit is put at the top). Illustrated above is the lattice configuration for computing .

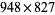Before the actual multiplication can begin, lines must be drawn for every diagonal path in the lattice from upper right to lower left to bisect each cell. There will be 5 diagonals for our 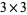 lattice array.

Now we calculate a product for each cell by multiplying the digit at the top of the column and the digit at the right of the row. The tens digit of the product is placed above the diagonal that passes through the cell, and the units digit is put below that diagonal. If the product is less than 10, we enter a zero above the diagonal.

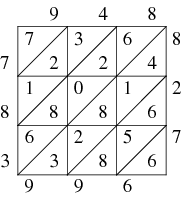
Now we are ready to calculate the digits of the product. We sum the numbers between every pair of diagonals and also between the first (and last) diagonal and the corresponding corner of the lattice. We start at the bottom half of the lower right corner cell (6). This number is bounded by the corner of the lattice and the first diagonal. Since this is the only number below this diagonal, the first sum is 6. We place the sum along the bottom of the lattice below the rightmost column.

Next we sum the numbers between the previous diagonal and the next higher diagonal: 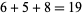. We place the 9 just below the bottom of the lattice and carry the 1 into the sum for the next diagonal group. (The diagonals are extended for clarity.)

We continue summing the groups of numbers between adjacent diagonals, and also between the top diagonal and the upper left corner. The final product is composed of the digits outside the lattice which were just calculated. We read the digits down the left side and then towards the right on the bottom to generate the final answer: 783996.

Although the process at first glance appears quite different from long multiplication, the lattice method is actually algorithmically equivalent.