المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lucas Polynomial Sequence |
 1851
 05:25 مساءً
date: 19-9-2019 |
Author : Horadam, A. F. 
Book or Source : "Extension of a Synthesis for a Class of Polynomial Sequences." Fib. Quart. 34 
Page and Part : ...|
Read More
Date: 17-9-2018
1939
Date: 16-8-2019
3299
Date: 22-4-2019
1325
|
A Lucas polynomial sequence is a pair of generalized polynomials which generalize the Lucas sequence to polynomials is given by
 |
 |
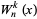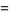![(Delta^k(x)[a^n(x)-(-1)^kb^n(x)])/(Delta(x))](http://mathworld.wolfram.com/images/equations/LucasPolynomialSequence/Inline3.gif) |
(1) |
 |
 |
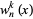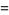![Delta^k(x)[a^n(x)+(-1)^kb^n(x)],](http://mathworld.wolfram.com/images/equations/LucasPolynomialSequence/Inline6.gif) |
(2) |
where
 |
 |
 |
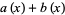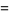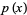(3) |
 |
 |
 |
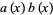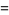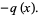(4) |
Solving for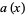 
and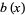 
and taking the solution for 
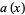with the 
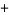sign gives
 |
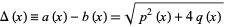(5) |
(Horadam 1996). Setting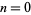 
gives
 |
 |
 |
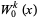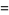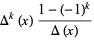(6) |
 |
 |
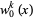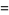![Delta^k(x)[1+(-1)^k],](http://mathworld.wolfram.com/images/equations/LucasPolynomialSequence/Inline23.gif) |
(7) |
giving
 |
 |
 |
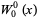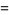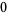(8) |
 |
 |
 |
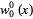(9) |
The sequences most commonly considered have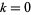 
, giving
![W_n(x)=W_n^0(x)=(a^n(x)-b^n(x))/(a(x)-b(x))
=([p(x)+sqrt(p^2(x)+4q(x))]^n-[p(x)-sqrt(p^2(x)+4q(x))]^n)/(2^nsqrt(p^2(x)+4q(x)))
w_n(x)=w_n^0(x)=a^n(x)+b^n(x)
=([p(x)+sqrt(p^2(x)+4q(x))]^n+[p(x)-sqrt(p^2(x)+4q(x))]^n)/(2^n).](http://mathworld.wolfram.com/images/equations/LucasPolynomialSequence/NumberedEquation2.gif) |
(10) |
The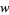 
polynomials satisfy the recurrence relation
 |
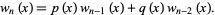(11) |
Special cases of the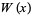 
and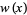 
polynomials are given in the following table.
 |
 |
 |
 |
 |
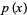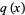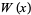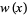1 | Fibonacci polynomial  |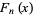
Lucas polynomial  |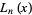
 |
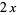1 | Pell polynomial  |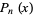
Pell-Lucas polynomial  |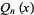
| 1 |  |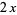
Jacobsthal polynomial  |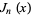
Jacobsthal-Lucas polynomial  |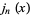
 |
 |
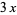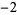Fermat polynomial  |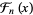
Fermat-Lucas polynomial  |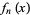
 |
 |
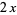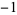Chebyshev polynomial of the second kind  |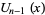
Chebyshev polynomial of the first kind  |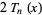
 |
 |
 |
 |
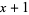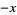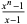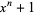REFERENCES:
Horadam, A. F. "Extension of a Synthesis for a Class of Polynomial Sequences." Fib. Quart. 34, 68-74, 1996.
|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|
