Power

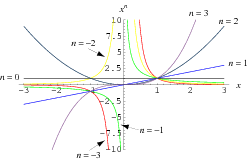
A power is an exponent to which a given quantity is raised. The expression 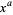 is therefore known as " to the 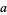th power." A number of powers of  are plotted above (cf. Derbyshire 2004, pp. 68 and 73).

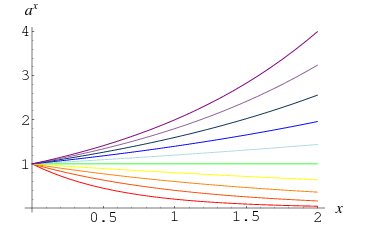
The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, 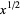 is real only for .

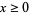A number other than 0 taken to the power 0 is defined to be 1, which follows from the limit

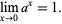(1)

This fact is illustrated by the convergence of curves at 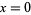 in the plot above, which shows  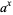for 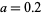, 0.4, ..., 2.0. It can also be seen more intuitively by noting that repeatedly taking the square root of a number  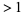gives smaller and smaller numbers that approach one from above, while doing the same with a number between 0 and 1 gives larger and larger numbers that approach one from below. For  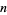square roots, the total power taken is 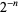, which approaches 0 as  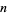is large, giving  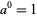in the limit that  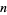is large.

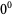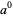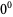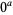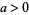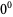 (zero to the zeroth power) itself is undefined. The lack of a well-defined meaning for this quantity follows from the mutually contradictory facts that  is always 1, so  should equal 1, but  is always 0 (for ), so  should equal 0. The choice of definition for  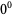is usually defined to be indeterminate, although defining  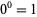allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57).

A number to the first power is, by definition, equal to itself, i.e.,

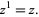(2)

Similarly,

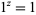(3)

for any complex number 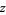. It is therefore impressive that Captain Kirk (William Shatner) is able to detect one more heartbeat aboard the starship Enterprise than can be accounted for by amplifying an auditory sensor intensified by a factor of "1 to the fourth power" in the Season 1 Star Trek episode "Court Martial" (1967).

The rules for combining quantities containing powers are called the exponent laws, and the process of raising a base to a given power is known as exponentiation.

The derivative of 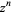 is given by

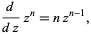(4)

and the indefinite integral by

(5)

The definite integral for  real is known as Cavalieri's quadrature formula and is given by

(6)

While the simple equation

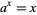(7)

cannot be solved for  using traditional elementary functions, the solution can be given in terms of the Lambert W-function as

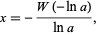(8)

where 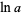 is the natural logarithm of .

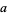Similarly, the solution to

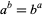(9)

can be solved for 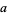 in terms of  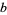using the Lambert W-function. In the special case 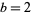, in addition to the solutions  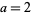and 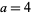, a third solution is

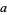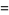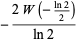			(10)
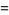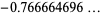			(11)

(OEIS A073084).

Special names given to various powers are listed in the following table.

power	name
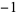	reciprocal
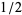	square root
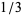	cube root
1	identity function
2	squared
3	cubed

Expressions of the form 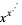 are known as power towers.

The largest powers 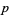 which numbers 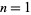, 2, 3, ... can be represented in the form  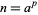are 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, ... (OEIS A052409), with corresponding values of  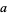given by 1, 2, 3, 2, 5, 6, 7, 2, 3, 10, ... (OEIS A052410).

A double binomial sum gives the power function as follows,

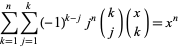(12)

(K. MacMillan, pers. comm., Nov. 14, 2007).

The power sum of the first 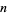 positive integers is given by Faulhaber's formula,

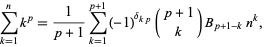(13)

where 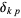 is the Kronecker delta,  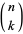is a binomial coefficient, and  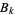is a Bernoulli number.

Let 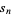 be the largest integer that is not the sum of distinct 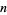th powers of positive integers (Guy 1994). The first few values for 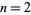, 3, ... are 128, 12758, 5134240, 67898771, ... (OEIS A001661).

Catalan's conjecture (now a theorem) states that 8 and 9 (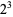 and 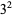) are the only consecutive powers (excluding 0 and 1), i.e., the only solution to Catalan's Diophantine problem. In addition, Hyyrő and Makowski proved that there do not exist three consecutive powers (Ribenboim 1996).

Very few numbers of the form 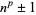 are prime (where composite powers  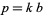need not be considered, since 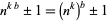). The only prime numbers of the form  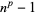for 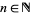 and prime  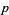correspond to  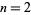and the Mersenne primes, i.e., 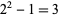, , 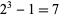, 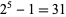.... Other numbers of the form  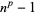equal 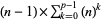. The only prime numbers of the form  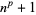for 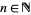 and prime  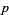correspond to  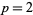with 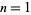, 2, 4, 6, 10, 14, 16, 20, 24, 26, ... (OEIS A005574). Other numbers of the form  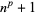equal .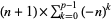

There are no nontrivial solutions to the equation

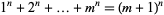(14)

for 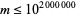 (Guy 1994, p. 153).

REFERENCES:

Barbeau, E. J. Power Play: A Country Walk through the Magical World of Numbers. Washington, DC: Math. Assoc. Amer., 1997.

Beyer, W. H. "Laws of Exponents." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 158 and 223, 1987.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Guy, R. K. "Diophantine Equations." Ch. D in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 137, 139-198, and 153-154, 1994.

Knuth, D. E. "Two Notes on Notation." Amer. Math. Monthly 99, 403-422, 1992.

Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 57, 1997.

Ribenboim, P. "Catalan's Conjecture." Amer. Math. Monthly 103, 529-538, 1996.

Sloane, N. J. A. Sequences A001661/M5393, A005574/M1010, A052409, A052410, and A073084 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Integer Powers 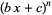 and 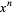" and "The Noninteger Powers 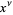." Ch. 11 and 13 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 83-90 and 99-106, 1987.