Riemann-von Mangoldt Formula

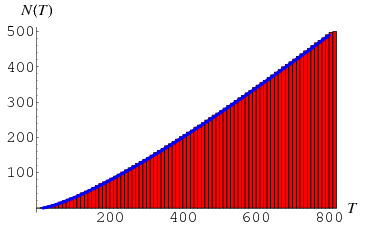
In his famous paper of 1859, Riemann stated that the number 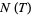 of Riemann zeta function zeros  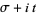with 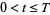 is asymptotically given by

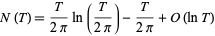(1)

as 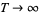 (Edwards 2001, p. 19; Havil 2003, p. 203; Derbyshire 2004, p. 258). This can be written more compactly as

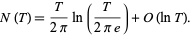(2)

This result was proved by von Mangoldt in 1905 and is hence known as the Riemann-von Mangoldt formula.

It follows that the density 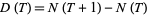 of zeros at height  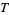is

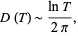(3)

where, as usual, the asymptotic notation 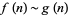 means that the ratio  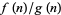tends to 1 as .

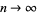Another consequence of this result is that the imaginary parts of consecutive zeta zeros in the upper half-plane 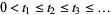 satisfy

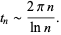(4)

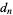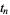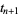Thus the mean spacing  between  and  is

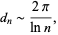(5)

which tends to zero as .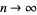

REFERENCES:

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, p. 217, 2004.

Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 138, 2003.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Ivic, A. A. The Riemann Zeta-Function. New York: Wiley, pp. 17-20, 1985.

Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.

Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.