Square Root

Min Max

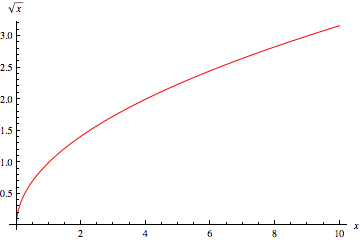A square root of  is a number 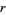 such that 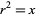. When written in the form  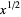or especially 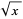, the square root of may also be called the radical or surd. The square root is therefore an nth root with .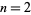

Note that any positive real number has two square roots, one positive and one negative. For example, the square roots of 9 are 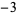 and 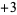, since 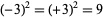. Any nonnegative real number  has a unique nonnegative square root 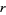; this is called the principal square root and is written  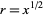or 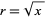. For example, the principal square root of 9 is 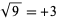, while the other square root of 9 is 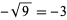. In common usage, unless otherwise specified, "the" square root is generally taken to mean the principal square root. 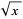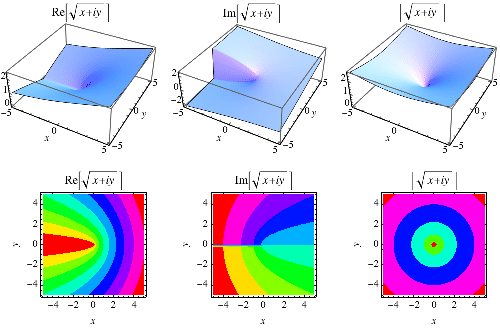The principal square root function is the inverse function of 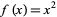 for .

Min   Max       Re       Im

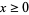Any nonzero complex number 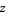 also has two square roots. For example, using the imaginary unit i, the two square roots of  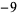are 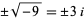. The principal square root of a number  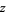is denoted  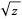(as in the positive real case) and is returned by the Wolfram Language function Sqrt[z].

When considering a positive real number , the Wolfram Language function Surd[x, 2] may be used to return the real square root.

The square roots of a complex number 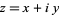 are given by

(1)

In addition,

(2)

As can be seen in the above figure, the imaginary part of the complex square root function has a branch cut along the negative real axis.

There are a number of square root algorithms that can be used to approximate the square root of a given (positive real) number. These include the Bhaskara-Brouncker algorithm and Wolfram's iteration. The simplest algorithm for 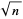 is Newton's iteration:

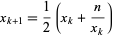(3)

with .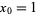

The square root of 2 is the irrational number 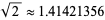 (OEIS A002193) sometimes known as Pythagoras's constant, which has the simple periodic continued fraction [1, 2, 2, 2, 2, 2, ...] (OEIS A040000). The square root of 3 is the irrational number  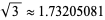(OEIS A002194), sometimes known as Theodorus's constant, which has the simple periodic continued fraction [1, 1, 2, 1, 2, 1, 2, ...] (OEIS A040001). In general, the continued fractions of the square roots of all positive integers are periodic.

A nested radical of the form 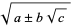 can sometimes be simplified into a simple square root by equating

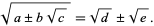(4)

Squaring gives

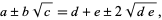(5)

so

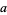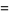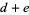			(6)
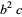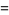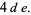			(7)

Solving for 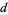 and 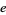 gives

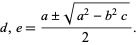(8)

For example,

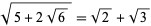(9)

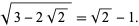(10)

The Simplify command of the Wolfram Language does not apply such simplifications, but FullSimplify does. In general, radical denesting is a difficult problem (Landau 1992ab, 1994, 1998).

A counterintuitive property of inverse functions is that

(11)

so the expected identity (i.e., canceling of the 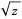s) does not hold along the negative real axis.

REFERENCES:

Landau, S. "A Note on 'Zippel Denesting.' " J. Symb. Comput. 13, 31-45, 1992a.

Landau, S. "Simplification of Nested Radicals." SIAM J. Comput. 21, 85-110, 1992b.

Landau, S. "How to Tangle with a Nested Radical." Math. Intell. 16, 49-55, 1994.

Landau, S. "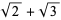: Four Different Views." Math. Intell. 20, 55-60, 1998.

Sloane, N. J. A. Sequences A002193/M3195, A002194/M4326, A040000, and A040001 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Square-Root Function 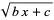 and Its Reciprocal," "The  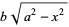Function and Its Reciprocal," and "The  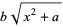Function." Chs. 12, 14, and 15 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 91-99, 107-115, and 115-122, 1987.

Williams, H. C. "A Numerical Investigation into the Length of the Period of the Continued Fraction Expansion of 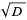." Math. Comput. 36, 593-601, 1981.